Indice dei contenuti
 Soluzione, considerazioni e approfondimenti suggeriti sul quesito posto da Paolo Alessandrini nella rubrica Moebius pubblicata su Coelum 180 di aprile
Soluzione, considerazioni e approfondimenti suggeriti sul quesito posto da Paolo Alessandrini nella rubrica Moebius pubblicata su Coelum 180 di aprile
La tavola rotonda di Dudeney
Nel 1907 Henry Dudeney, grande creatore di rompicapi e giochi matematici, propose il seguente problema: “Fate accomodare le stesse n persone a una tavola rotonda (n-1)(n-2)/2 diverse volte, in modo che nessuna persona abbia per più di una volta gli stessi due vicini”.
 L’enigma venne pubblicato, assieme a molti altri, nel libro “The Canterbury Puzzles”, uno dei grandi classici della matematica ricreativa.
L’enigma venne pubblicato, assieme a molti altri, nel libro “The Canterbury Puzzles”, uno dei grandi classici della matematica ricreativa.
L’immagine della tavola rotonda richiama subito alla mente i cavalieri della corte di re Artù, menzionati nelle leggende del ciclo bretone. Nelle diverse versioni, il numero di questi nobili personaggi varia molto, da 12 a oltre 150.
A noi, però, non importa quanti fossero i cavalieri: ci basta chiamare questo numero n.
Il problema di Dudeney suggerisce che esistano (n-1)(n-2)/2 diversi modi di accomodare i cavalieri a tavola, rispettando il vincolo per cui nessuno di loro ritroverà per più di una volta la stessa coppia di colleghi ai suoi due lati. Perché proprio (n-1)(n-2)/2?
Lo possiamo comprendere facilmente.
 In quanti modi possiamo riempire il posto alla destra di re Artù? Naturalmente in n-1 modi, perché possiamo collocare chiunque degli n cavalieri tranne lo stesso sovrano. E una volta occupato quel posto, quanti modi abbiamo di piazzare un commensale alla sinistra di Artù? Ovvio: n-2, perché a questo punto abbiamo già escluso 2 persone. Quindi esistono (n-1)(n-2) modi di riempire i due posti vicini all’illustre sovrano.
In quanti modi possiamo riempire il posto alla destra di re Artù? Naturalmente in n-1 modi, perché possiamo collocare chiunque degli n cavalieri tranne lo stesso sovrano. E una volta occupato quel posto, quanti modi abbiamo di piazzare un commensale alla sinistra di Artù? Ovvio: n-2, perché a questo punto abbiamo già escluso 2 persone. Quindi esistono (n-1)(n-2) modi di riempire i due posti vicini all’illustre sovrano.
Ma facciamo attenzione all’esatta formulazione del problema: ciascun cavaliere non deve ritrovarsi più volte la stessa coppia di vicini, indipendentemente dal fatto che siano scambiati di posto. Di conseguenza contando (n-1)(n-2) modi abbiamo in realtà contato ogni configurazione due volte: il numero giusto è quindi (n-1)(n-2)/2.
Per fortuna la matematica è democratica, per cui il ragionamento condotto per re Artù si applica pari pari a tutti i cavalieri. Possiamo allora concludere che il numero di configurazioni proposto da Dudeney è corretto.
Il numero (n-1)(n-2)/2 può essere ricavato anche attraverso un procedimento appena diverso. Il numero di possibili disposizioni degli n cavalieri corrisponde infatti al numero di modi in cui possiamo estrarre 2 elementi da un insieme di n-1 elementi.
Chi mastica un po’ di matematica sa che questo numero è espresso dal coefficiente binomiale “n su 2”, cioè:
Per fortuna abbiamo ritrovato lo stesso numero di prima!
Vabbè: ma adesso, che ce ne facciamo di questo bel numerino? Sapere quanti sono i modi di far sedere i cavalieri non significa conoscere nel dettaglio tutte queste disposizioni.
D’altra parte la determinazione di queste configurazioni costituisce il vero rompicapo di Dudeney.
Il problema è stato risolto per qualsiasi n pari, ma non ha una soluzione generale se n è dispari. Ai tempi di Dudeney (che morì nel 1930), per esempio, non era nota alcuna soluzione per il caso n = 13, che richiama alla memoria l’ultima cena di Gesù.
Lo stesso matematico inglese descrisse in dettaglio tutte le soluzioni dell’enigma per n compreso tra 3 (numero minimo di commensali per il quale il problema ha senso) e 12.
Ad esempio, la figura seguente illustra le soluzioni (uniche) per n uguale a 3, 4, e 5.
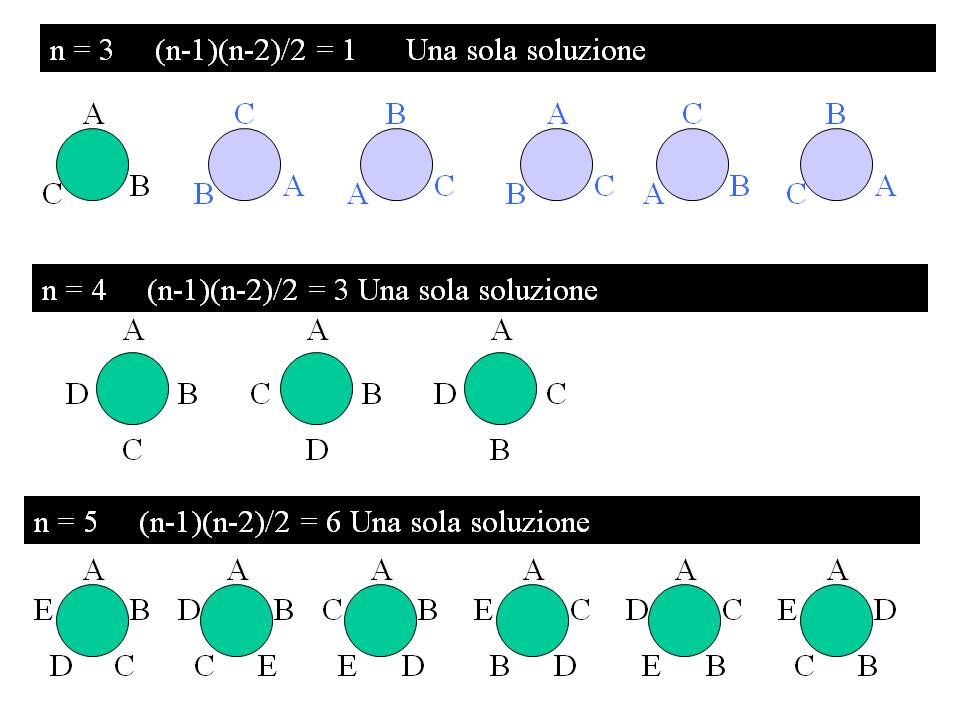 Dagli anni Sessanta in poi, il problema venne preso in grande considerazioni da diversi matematici e risolto per valori più alti di n, anche sfruttando algoritmi informatici.
Dagli anni Sessanta in poi, il problema venne preso in grande considerazioni da diversi matematici e risolto per valori più alti di n, anche sfruttando algoritmi informatici.
Ad oggi, il valore più basso di n per il quale non è nota alcuna soluzione è 41: si sa che le configurazioni in questo caso sono (41-1)(41-2)/2 = 780, ma nessuno sa quali siano di preciso.
L’intricato caso dei governatori galattici
Anche se ambientato in un contesto fantascientifico e non nello scenario delle leggende anglosassoni, l’enigma del numero 180 di Moebius era una riformulazione del classico problema di Dudeney.
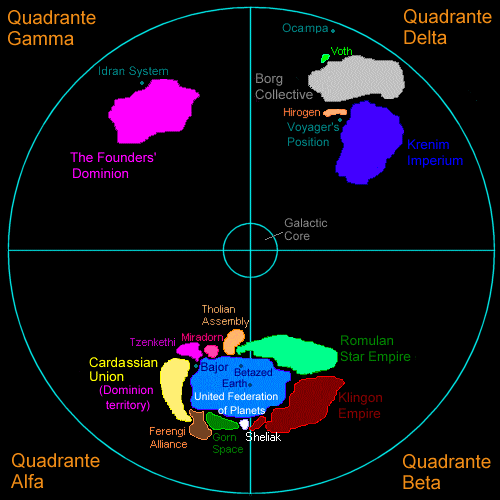 Al posto della tavola rotonda c’è la Via Lattea, e i commensali sono sostituiti dai settori galattici amministrati da altrettanti governatori. Con i quattro quadranti alla Star Trek la soluzione è semplice: anzi, l’avete già vista nella figura precedente.
Al posto della tavola rotonda c’è la Via Lattea, e i commensali sono sostituiti dai settori galattici amministrati da altrettanti governatori. Con i quattro quadranti alla Star Trek la soluzione è semplice: anzi, l’avete già vista nella figura precedente.
Con n = 4 abbiamo (n-1)(n-2)/2 = (4-1)(4-2)/2 = 3 disposizioni possibili.
Ad esempio, se i governatori sono A, B, C e D, lo schema di rotazione che risolve il problema è il seguente:
A B C D
A B D C
A C B D
Si noti che in ciascuna disposizione l’ultimo governatore (quello indicato a destra) sarà vicino al primo (quello più a sinistra). Questo significa che ad esempio la prima configurazione A B C D può indifferentemente essere scritta anche come B C D A, oppure C D A B, oppure D A B C.
Tenendo conto di questo fatto, potrete constatare che con n = 4 non vi sono altre soluzioni del problema.
Con sei settori, la faccenda si fa più complicata. Lo ammetto: questa volta sono stato cattivello, e infatti nessuno, per la prima volta nella storia della rubrica (che ormai si accinge a festeggiare il suo primo compleanno), è riuscito ad aggiudicarsi l’abbonamento semestrale.
Una nostra vecchia conoscenza, però, è riuscita a risolvere il rompicapo: Maurizio Carlino. Il provetto risolutore di problemi non è stato menzionato in calce alla rubrica del numero 182, perché la sua risposta è arrivata quando l’articolo era già prossimo alla stampa. E comunque Carlino aveva già vinto l’abbonamento in precedenza, e quindi la sua partecipazione (come lui stesso aveva sottolineato) era fuori concorso.
Mi scuso comunque con Carlino per non averlo citato nella rubrica di maggio, e mi complimento con lui per la sua brillante impresa.
Com’è ormai sua abitudine, il nostro affezionato lettore ci ha inviato un’analisi dettagliata del problema, corredata dalla soluzione e da una spiegazione approfondita del procedimento adottato per ottenerla.
Come si risolve la parte difficile del problema, cioè lo schema di rotazione dei 6 governatori? In questo caso le possibili configurazioni sono (6-1)(6-2)/2 = 10, ma quali sono?
Trovarle “a mano” era possibile, ma non semplice. Un programma informatico sicuramente rappresentava una via più agevole, e non a caso questo è stato il procedimento scelto da Carlino.
Identificando i governatori con le prime 6 lettere dell’alfabeto, la soluzione proposta dal nostro lettore-risolutore è la seguente:
A B C D E F
A B D C F E
A B E D F C
B D E A F C
B D F A C E
A D B F C E
A C D F B E
D C E F B A
C B E F D A
C B F A D E
Nella tabella seguente, inviataci dal nostro lettore, vengono evidenziate le coppie di vicini di ogni governatore in ciascuna delle 10 configurazioni.
Naturalmente questa è una delle molte soluzioni possibili del problema con n = 6: a differenza del caso con n = 4, infatti, la soluzione non è affatto unica.
Non contento di aver comunque risolto il problema “base”, Carlino ha analizzato il numero di spostamenti necessari per passare da una configurazione a quella successiva.
Nella soluzione esposta sopra, questo numero è sempre 3, tranne che per il primo passaggio, nel quale sono necessari 4 spostamenti. Il numero totale di spostamenti è quindi pari a 28.
Ci scrive Carlino:
“Non sono riuscito a trovare una soluzione che presenti un numero inferiore di spostamenti, ma non dispongo di una dimostrazione matematica del fatto che 28 sia il valore minimo. Sarà molto interessante scoprire se qualcun altro è stato capace di produrre una soluzione a ‘costo’ inferiore; al momento posso solo dire che il mio algoritmo non ha trovato soluzioni inferiori a 28 con il vincolo di usare ad ogni passo una nuova configurazione che differisse dalla precedente di al più 4 spostamenti. In particolare non sono riuscito a trovare soluzioni con costo totale = 27 in cui tutte le 9 configurazioni avessero un costo pari a 3 e neppure almeno una soluzione in cui compaia una configurazione di costo 2 seppur teoricamente compatibile con i vincoli del problema.”
Giro l’interessante sfida ai lettori e ai visitatori!
In conclusione, complimenti a tutti i lettori che hanno affrontato il problema e in particolare al bravissimo Maurizio Carlino.
Al prossimo enigma!








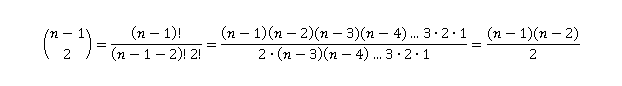













Spett. Ing. Alessandrini, mi sto chiedendo a cosa servano nella vita di qualunque persona, astrofilo o non, questi tipi di “rompicapo”. Le posso rispondere in un solo modo: …….ma mi faccia un piacere!!!!
Marco la domanda che fai può anche essere lecita, ma il commento finale è assolutamente fuori luogo…
La scelta di avere una pagina di questo tipo è stata della Redazione: Paolo fa questo di lavoro e noi gli abbiamo chiesto di curare una rubrica di questo tipo per noi, perché piace, perché diverte, perché interessa e interessa a molti lettori anche tutto il percorso matematico e spesso storico che Paolo sviluppa attorno ad ogni quesito.
Come dice Giorgia per cultura personale, per elasticità mentale, ma anche solo per divertimento e per mettere alla prova le proprie capacità logiche.
Cosa che piace molto, la logica matematica, l’enigmistica, a chi si interessa in generale di scienza.
E Coelum si rivolge agli astrofili ma non solo, anche a chi astrofilo non è ma è interessato all’astronomia, all’astronautica, alla storia dell’astronomia, etc…
Se a qualcuno non piace è solo una pagina su 84 in meno da leggere, così come a molti non interessano per nulla le dieci pagine di effemeridi, o le due sugli asteroidi, o l’astronautica, o le quattro dedicate ad un articolo di approfondimento storico… ma non per questo vanno a screditarne gli autori.
Sbeffeggiarlo solo perché a te non interessa o non lo capisci non mi pare proprio il caso.
Al più, se proprio vuoi… puoi criticare la scelta della redazione, argomentando però, non sbeffeggiando…
Cultura personale ed elasticità mentale…
Per la cultura a la elasticità mentale abbiamo già “La settimana enigmistica”, in edicola, questa non era “comunque” la sede per gli indovinelli e per i “rompicapo”. Saluti.
Spett. Paola, chiede solo di “argomentare”?….. allora “argomentiamo”. Perchè piuttosto che pagine di “indovinelli”, che a pochi interessano, e che ben pochi tra l altro, sanno risolvere, non inserite trattati del CICAP? Questo sarebbe già un settore che a molti interessa, e che, a quanto sembra lei “ne sa qualcosa”. Potrebbe aiutare, anche in qualche modo, questo Comitato a non “chiudere i battenti”, per mancanza di sostenitori, dalle notizie che si hanno in rete. Saluti.
eh… ti stupirà invece sapere che tra i nostri lettori c’è più gente interessata agli enigmi logici che al pensiero critico. Anzi, c’è chi non solo non è interessato al CICAP, ma è proprio inviperito ogni volta che pubblichiamo qualcosa che lo riguarda…
Ma vedi… la logica è un’arma importante soprattutto per veicolare e sviluppare, divertendo, il pensiero critico (e infatti anche la rivista del CICAP, Query, ha una pagina esattamente di questo tipo, su engimi logici e illusioni ottiche, adattata ovviamente al tipo di argomenti e lettori di quella rivista, come Paolo fa con la nostra).
Quanto al CICAP, quando abbiamo argomenti di interesse comune non manchiamo di pubblicare loro interventi, e pubblicizziamo sempre le loro iniziative più importanti. Come abbiamo fatto appunto con Luca Boschini e il libro edito dal CICAP “Cosmonauti perduti”, o con il libro di Paolo Attivissimo “Luna? Si, ci siamo andati”, che è presente anche all’interno del nostro DVD Coelum 9, in versione sfogliabile proprio come la nostra rivista digitale, pubblicando spesso le loro inserzioni, etc…
Quando possiamo il nostro lo facciamo, così come loro danno una mano a noi quando è possibile (siamo tutti nella “stessa barca”…).