ATMOS e l’Optical Design

Agli inizi del XVII secolo vi fu una vivace disputa sulla paternità dell’invenzione di un singolare strumento capace di ‘avvicinare’ oggetti lontani grazie ad un’appropriata combinazione di semplici lenti. Ne furono protagonisti l’occhialaio Jan Lippershey di Middelbourg e James Metius di Alkmaar, entrambi autori di una specifica petizione diretta agli Stati Generali olandesi per assicurarsene il brevetto, e forse anche un terzo contendente, Zacharias Jansen. Al di là dei dubbi e delle contese, l’aspetto più rilevante è che nel 1609 Galileo Galilei, durante il suo soggiorno patavino, riuscì a ricostruirne uno, lo chiamò cannocchiale e lo rivolse verso il cielo, segnando in quel momento l’inizio della moderna Astronomia telescopica e di fatto una grande rivoluzione per la Scienza. In principio si trattava di strumenti dalle prestazioni modeste e per decenni le migliorie apportate o suggerite da Kepler, Descartes, Hevelius e Huygens potevano essere considerate piuttosto come il frutto di applicazioni empiriche. I lunghi rifrattori e i nuovi riflettori con specchi in leghe metalliche nati verso la fine di quel periodo e a cavallo del XVIII secolo presentavano limitazioni nell’ampiezza di campo utile e nella qualità delle immagini non legate solo alle procedure di fabbricazione degli obiettivi, ma soprattutto alla presenza di aberrazioni inerenti agli schemi ottici adottati, causate dal comportamento della luce al loro interno e non ancora perfettamente comprese dal punto di vista fisico. La correzione di questi difetti richiedeva un approccio analitico più rigoroso, che cominciò ad apparire nei lavori di ottica teorica di Isaac Newton (1666) e tese a perfezionarsi in quelli successivi di Dollond, il primo a costruire un obiettivo acromatico sulla base di calcoli geometrico-matematici. Altri importanti contributi vennero poi da Fraunhofer, Wollaston, Coddington, Hamilton e Gauss. Deposti i monumentali telescopi di William Herschel, bisognerà giungere al 1840 per avere con Petzval un primo esempio di applicazione generale dei metodi matematici al tema della progettazione di lenti, questa volta destinate ad una nuova straordinaria tecnica di fare immagini, la fotografia, seguito poco più tardi dalla pubblicazione della  teoria delle aberrazioni di Seidel, distinte in due cromatiche, l’aberrazione cromatica longitudinale e quella laterale, e in cinque monocromatiche di terzo ordine, l’aberrazione di sfericità, di coma, l’astigmatismo, la curvatura di campo e la distorsione. Il progressivo affinamento di queste metodiche portò ben presto all’affermazione della nuova disciplina scientifica dell’Optical Design, la quale mira a sviluppare, controllare e ottimizzare sistemi diottrici, catottrici o catadiottrici in grado di creare immagini del mondo reale grazie alle proprietà fisiche della luce, nonché di misurare quantitativamente o di analizzare qualitativamente la radiazione luminosa su un ampio range spettrale. Se per la parte di lavoro del progettista che consiste nel valutare le prestazioni dell’obiettivo a mano a mano che il progetto evolve la teoria delle aberrazioni di Seidel rappresentava di sicuro un valido ausilio, per altri versi si rendeva necessaria un’analisi molto più approfondita della struttura dell’immagine in formazione, utilizzando metodi basati sulla trigonometria e su specifiche leggi, come quella di Snell sulla rifrazione e la riflessione della luce. Ricordiamo che per la prima esiste un rapporto fra l’angolo formato da un raggio di luce con la normale della superficie ottica (ε) e quello del raggio rifratto (ε¹) secondo la relazione:

sin e /sin ε¹ = n¹ / n

dove ( n ed n¹) sono gli indici di rifrazione dei mezzi attraversati dalla luce, ad esempio un vetro ottico di una lente e l’aria. La seconda, invece, afferma che l’angolo di incidenza (i) di un raggio di luce su una superficie speculare è uguale a quello di riflessione (i¹) in base alla relazione:

i = -i¹

Anche il telescopio, come tutti i sistemi ottici, obbedisce a queste due leggi.

Sappiamo che esso è composto da lenti o specchi o entrambi le cui funzioni principali sono il potere risolutivo, cioè la capacità di separare particolari od oggetti tra loro angolarmente molto vicini, considerando i fenomeni connessi alla natura ondulatoria della luce, e quella di aumentare la quantità di luce raccolta che raggiunge il recettore (occhio, pellicola fotografica o sensore digitale). Nonostante la complessa natura della luce, a proposito della quale si parla di onde, particelle e pacchetti di fotoni, nel calcolo e nella progettazione dei sistemi basati su ottiche geometriche si fa riferimento a raggi o a fasci di raggi luminosi, ognuno dei quali è seguito lungo una direzione lineare quando penetra nel sistema ottico, finché non incontra un ostacolo o attraversa un mezzo con caratteristiche dispersive particolari (aria, vetro) e subisce gli effetti di fenomeni come la diffrazione, la rifrazione o l’interferenza. Insieme con i raggi nell’Optical Design si parla anche di fronti d’onda per indicare superfici curve, fisiche o geometriche, normali ai primi. Nel caso di una sorgente luminosa puntiforme e di un mezzo omogeneo che abbia un indice di rifrazione costante i raggi luminosi si possono rappresentare come linee diritte divergenti da quel punto, mentre i fronti d’onda hanno forma sferica con il centro di curvatura sull’oggetto. Un buon sistema ottico deve essere in grado di raccogliere raggi e fronti d’onda della sorgente-oggetto e reindirizzarli, nella maniera più fedele e inalterata possibile, verso i corrispondenti punti e centri di curvatura dell’immagine, ossia sul piano focale dell’obiettivo. La valutazione matematica e qualitativa di questo durante la fase di progettazione richiede il tracciamento di molti raggi geometrici reali o trigonometrici (ray-tracing), che attraversano il sistema ottico, partendo dalla sorgente luminosa e giungendo sul piano ove si forma l’immagine. Per ciascun raggio si applica la legge di Snell, via via che esso incontra le varie superfici con calcoli ripetuti per ogni raggio e per ogni superficie, con i risultatiottica raggiunta negli stadi iniziali del progetto. I termini “ primo e terzo ordine” fanno riferimento a certe proprietà delle funzioni trigonometriche, dal momento che le aberrazioni ottiche dipendono in misura rilevante dagli angoli dell’immagine, soprattutto dalle funzioni del seno e della tangente. Un pregio del metodo di Seidel è che il progettista può  trattare ogni singola aberrazione in luce monocromatica con un calcolo a sé stante, così che diventa facile individuare quale superficie aberrata all’interno dello schema ottico abbia dato il maggior contributo alla formazione dell’immagine non perfetta; 3) il calcolo o disegno del raggio meridionale, un esatto ray-tracing nel quale il percorso di ciascun raggio è calcolato attraverso gli elementi ottici, utilizzando le leggi della rifrazione e della riflessione. Il ray-tracing meridionale è ristretto al piano che passa dal centro degli elementi ottici dell’obiettivo, talvolta detto piano meridionale o tangenziale; 4) infine il tracciamento dei raggi d5113055  raccolti in apposite tabelle. Agli albori dell’Optical Design l’esecuzione di questi calcoli avveniva manualmente con grande dispendio di tempo e di risorse; in seguito si utilizzarono il sistema dei logaritmi e le calcolatrici meccaniche (1930), finché l’avvento del computer (1960) pose fine alle applicazioni manuali e non solo favorì la velocizzazione dei calcoli e delle operazioni geometriche, ma permise anche la creazione di nuovi algoritmi che consentivano di modificare liberamente i parametri dell’obiettivo allo scopo di migliorarne le prestazioni. In sostanza, partendo da una configurazione iniziale, con il computer divenne possibile ottimizzare l’obiettivo attraverso un processo iterativo facilmente controllabile, al termine del quale il progettista aveva la ragionevole sicurezza che la qualità dell’immagine raggiunta fosse la migliore che quell’obiettivo poteva fornire, tenuto conto della configurazione ottica di base, della focale, dell’apertura relativa, del campo di visione, delle lunghezze d’onda selezionate o dei valori di ostruzione scelti. Altra importante conseguenza fu la riqualificazione degli schemi ottici più tradizionali elaborati nei secoli precedenti, i quali potevano essere ricalcolati per ottenere prestazioni più esaltanti o per semplificare i processi di produzione o ancora per sperimentare le caratteristiche di nuovi tipi di vetro ottico naturale o sintetico o, infine, per sviluppare schemi ottici più complessi e innovativi con una maggiore riduzione delle aberrazioni, un miglioramento del potere di contrasto e della definizione grazie all’impiego di vetri con materiali dalle migliori proprietà dispersive e rifrattive o che apparissero più in sintonia con le qualità di imaging dei nuovi rivelatori a stato solido anche nelle regioni estreme dello spettro elettromagnetico.

In linea generale le fasi nelle quali più comunemente si articola l’Optical Design sono:

1) il calcolo parassiale o calcolo di primo ordine.
E’ un metodo applicato per le regioni vicine all’asse ottico entro piccolissime distanze e angoli fuori asse. Esso fornisce la posizione dei piani principali, la lunghezza focale del sistema, informazioni sui raggi di curvatura, gli spessori e le distanze degli elementi ottici, mentre non offre nessun dato relativo alle aberrazioni ottiche.
2) il calcolo di Seidel o di terzo ordine.
Permette al progettista di analizzare i tipi e considerare il peso delle aberrazioni eventualmente presenti, per compiere una rapida valutazione della qualit_liqui (skew ray-tracing), un metodo nel quale si determinano i percorsi di un grande numero di raggi che coprono l’intera pupilla di entrata dell’obiettivo al fine di produrre dei diagrammi a macchie e mostrare con estremo rigore il tipo di immagine finale che il sistema ottico potrà produrre.

Nel configurare un sistema ottico il progettista deve determinare alcuni requisiti fondamentali: ad esempio la natura e combinazione delle ottiche, il livello delle prestazioni da raggiungere, la destinazione d’uso finale, le caratteristiche meccaniche, le variabili che egli è in grado di controllare, la tipologia degli strumenti di registrazione e analisi dell’immagine ai quali l’obiettivo andrà applicato.
Ad una visione generale dovrebbe far seguire un esame più dettagliato:

1. delle proprietà del sistema di primo ordine
   Esse includono il diametro della pupilla d’entrata (E.P.D.), la lunghezza focale (F), il rapporto focale (f), l’ingrandimento (i), il campo di visione (F.O.V.), lo spazio della cosidetta back focal lenght (B.F.L.), il range di lunghezze d’onda scelte per l’analisi del sistema ottico o per l’osservazione migliore.
2. dei requisiti dell’imaging
   Questo aspetto riguarda il livello di dettaglio nell’oggetto che deve essere registrato. Le misure dirette sulla qualità dell’immagine comprendono le dimensioni geometriche delle macchie nei relativi diagrammi, l’errore geometrico di fronte d’onda, la risoluzione angolare limite, il trasferimento di contrasto ad una specifica frequenza spaziale calcolato attraverso la funzione di trasferimento della modulazione (M.T.F.), il rapporto Strehl, l ‘Encircled Energy Plot’ (E.E.P.). I requisiti di imaging determinano anche se il campo sarà piano o curvo e la quantità accettabile di distorsione per aberrazioni o diffrazione.
3. di ulteriori considerazioni particolari.
   Tra le considerazioni speciali troviamo dettagli tecnici tipici di strumenti di analisi della radiazione elettromagnetica come gli spettrografi, i fotometri, i coronografi, gli interferometri, i telescopi a raggi X o per l’infrarosso.

Il progettista ottico può controllare solo alcune variabili del sistema dette gradi di libertà. Un grado di libertà indica l’abilità di fare una libera scelta rispetto ad un parametro ottico: ad esempio può essere utile variare il raggio di curvatura di una lente o la distanza fra due superfici, ricalcolare l’asfericità di una superficie o scegliere un tipo di vetro piuttosto di un altro per via delle differenti proprietà dispersive. Un’efficace correzione delle aberrazioni di immagine di un sistema ottico impone al progettista di disporre di tanti gradi di libertà quanto è il numero di aberrazioni da eliminare. Spesso è necessario contare il numero di variabili che uno strumento ottico consente di cambiare durante le fasi di ottimizzazione del progetto, delle quali occorre stimare quante siano indipendenti ed effettive nel controllare le proprietà e le aberrazioni ottiche. Per i sistemi formati da superfici sferiche centrate le sole variabili sono: le curvature/raggi delle superfici, lo spazio/spessore tra le superfici, i tipi di vetro distinti per indici di rifrazione e dispersione cromatica, la posizione del diaframma all’interno dello schema ottico. Sistemi meno convenzionali hanno altre variabili, che derivano dall’uso di superfici asferiche, inclinate e decentrate, o da prismi o reticoli di diffrazione. Come già accennato, sebbene le formule e i calcoli conducano a soluzioni molto vicine al progetto finale, di norma è necessario un processo conclusivo di ottimizzazione dei sistemi elaborati, ricorrendo a tecniche di ray tracing via via più precise, così da ridurre al massimo le aberrazioni residue assiali ed extrassiali.
Il procedimento si svolge con prove ed errori, tenendo conto di questi e cercando di eliminarli un po’ alla volta, attraverso l’introduzione di piccole variazioni nei parametri ottici: ad esempio modificando la combinazione correttore-secondario nei catadiottrici o cambiando il raggio di curvatura del secondario, nel caso dei riflettori.

In conclusione il progettista al termine del suo lavoro dovrebbe avvicinarsi il più possibile ai criteri indicati da Maxwell per l’immagine perfetta:

1. nel caso di una sorgente luminosa puntiforme, tutti i raggi che attraversano il sistema ottico devono convergere in un’unica immagine puntiforme, cioè i punti devono essere riprodotti come punti;
2. se la superficie dell’oggetto-sorgente è un piano perpendicolare all’asse ottico, anche le corrispondenti immagini devono giacere su un piano normale a quell’asse, cioè il sistema ottico deve avere un campo piano;
3. linee diritte presenti sul piano dell’oggetto-sorgente devono essere riprodotte come linee diritte anche sul piano dell’immagine, cioè il sistema ottico deve essere privo di distorsioni o altre aberrazioni geometriche.

Se da un lato la gran parte delle case produttrici di strumenti ottici hanno sviluppato propri software di Optical Design con criteri direttamente legati alle fasi di creazione industriale dei loro obiettivi, a livello commerciale e ‘amatoriale’ evoluto, invece, i programmi più noti in cui è possibile usare ed approfondire molte delle funzioni prima sommariamente indicate sono OSLO, ZEMAX, MODAS, BEAM 4, TDESIGN, LENSDES e RAYTRACE, questi ultimi tre integranti l’ottimo testo “Telescope Optics” di H.Rutten e M.van Venrooij.

Da qualche anno troviamo accanto ad essi un altro straordinario software di Optical Design prodotto da Massimo Riccardi, ATMOS (Amateur Telescope Maker Optical designer and analysis Software), un programma nato con l’intento di ampliare le capacità offerte dalle funzioni presenti nel lavoro dei due ultimi autori citati, soprattutto con la possibilità di creare diagrammi a macchie per molte lunghezze d’onda contemporaneamente ed offrire all’utente una serie di strumenti di analisi e progettazione dei sistemi ottici completa, veloce, approfondita, flessibile, in grado di giungere a soluzioni tecniche innovative o di perfezionare quelle più tradizionali al fine di elaborare un obiettivo di alte prestazioni e garantire la migliore qualità delle immagini ottiche.

Compilato all’inizio in Qbasic, ATMOS fu in seguito sviluppato in ambiente Windows per poter disporre di una migliore veste grafica e di un’interfaccia utente più ‘amichevole’ grazie alla presenza di finestre, pulsanti e caselle utili all’immissione e alla visualizzazione dei vari dati. ATMOS, che consente di lavorare con sistemi ottici simmetrici per rotazione, assialmente centrati e fuori asse, contiene vari menu a tendine, dai quali si accede alle numerose operazioni di design e analisi delle principali configurazioni ottiche. Vediamole più in dettaglio.

Attraverso il menu (File) l’utente può scegliere tra la creazione di un nuovo progetto ottico, l’apertura di uno dei 36 già esistenti e il salvataggio di quello in corso. Nel primo caso viene visualizzata una tabella in cui andranno inseriti con esattezza alcuni dati preliminari di fondamentale importanza per la definizione teorica del sistema ottico, fra i quali il numero delle superfici (fino a 100, oltre al piano focale e ai cosidetti obscuration screens, ossia alle aree non illuminate presenti nel percorso dei raggi di luce prodotte da elementi ostruttivi), lo stop d’apertura, il semidiametro dell’obiettivo, il raggio di curvatura delle superfici (seguendo le indicazioni fornite nell’help circa la convenzione dei segni), lo spessore delle lenti misurato sull’asse centrale, il mezzo attraversato dalla luce (aria, vetro), il tipo di vetro ottico, scelto dai cataloghi Schott, (persino con riferimento ai nuovi “vetri ecologici” a basso contenuto di arsenico e piombo), Ohara, Hoya e Corning, l’indice di rifrazione, la figura della superficie (sferica, conica o di ordine superiore, come ad esempio può essere una lastra correttrice di Schmidt). E’ possibile selezionare fino a sei lunghezze d’onda operative (per le righe C, e, F del visibile, per la visione scotopica o per quella fotopica), il semidiametro del fascio luminoso in entrata, la distanza, finita o infinita, delle sorgenti, l’angolo di semicampo Alcuni di questi parametri possono essere inseriti anche utilizzando le funzioni di (Edit), come il numero delle superfici, le lunghezze d’onda o i valori lineari delle superfici non centrate e quelli angolari delle superfici inclinate. Una volta immesse queste informazioni numeriche, il programma esegue una serie di calcoli e fornisce i dati relativi alla B.F.L. (back focal lenght), alla lunghezza focale, all’altezza che il raggio principale raggiunge rispetto all’asse ottico sul piano focale e  al rapporto focale dell’obiettivo.

Nell’altro caso, invece, gli esempi presentati appaiono già completi e pronti per l’analisi ottica, che si effettua per mezzo delle funzioni contenute nel menu (Analysis).
Queste sono:

1) Detailed Spot Diagram (diagrammi a macchie dettagliati e policromatici con analisi della vignettatura)

Si tratta di particolari diagrammi nei quali, sulla base di complesse equazioni di ottica geometrica, si analizza un fascio di raggi luminosi monocromatici dentro un sistema ottico di lenti o specchi e si simulano le dimensioni, la forma e la distribuzione della luce proveniente da un oggetto puntiforme, come una stella, quando attraversa un obiettivo per giungere sul piano dell’immagine. Se si trascura la diffrazione, il diagramma costituisce una specie di mappa di tutti i punti di impatto dei fotoni sulla superficie dell’immagine, dando così una esatta visualizzazione della qualità di questa e delle eventuali irregolarità create dalle aberrazioni esistenti. Per i sistemi che formano immagini con luce policromatica o in cui sono impiegati vetri con differenti indici di rifrazione i raggi possono essere migliaia, in relazione alle lunghezze d’onda prescelte. ATMOS può tracciarne fino a 30000, 5000 per ognuno dei 6 colori considerati. L’analisi è condotta anche per i raggi provenienti con angoli fuori asse o a più lunghezze d’onda contemporaneamente, nel caso di lenti. Variando la posizione del piano focale  in avanti e indietro, è possibile esaminare l’effetto del fuocheggiamento sulla struttura del diagramma a macchie, al fine di fissare il cosidetto best focus, ossia la posizione in cui la messa a fuoco fornisce le immagini più puntiformi; la funzione consente anche di tener conto della percentuale di campo vignettato, cioè non del tutto illuminato, soprattutto ai bordi.

2) Multispot Diagram (through focus/field) (diagrammi multispot, in relazione al rapporto fuoco/campo)

Questi diagrammi a macchie sono ottenuti nello stesso tempo sull’asse ottico, sul 70% del campo di visione e sul 100% dello stesso, per diverse posizioni del piano focale, in modo da permettere al progettista di verificare le tolleranze di fuoco del sistema.

3) Matrix Spot Diagram (diagrammi a macchie di tipo matrix)

Sono diagrammi a macchie individuali per ciascuna lunghezza d’onda, visualizzate separatamente e poi comparate con le dimensioni dei corrispondenti dischi di Airy.

4) Total Field Spot Diagram (diagrammi a macchie a campo pieno)

In questo caso un grafico diviso in nove settori fornisce un quadro complessivo delle figure di diagrammi a macchie per angoli e distanze diverse dal centro asse, lungo le coordinate x-y.

5) R.M.S. spot size versus focus, field, wavelenght (dimensioni R.M.S. della macchia in relazione al fuoco, al campo di visione e alla lunghezza d’onda)

Si visualizza un grafico in cui è rappresentata sull’asse delle ordinate il raggio RMS (root mean square) della macchia confrontata con le dimensioni del disco di Airy e su quello delle ascisse la variazione positiva e negativa della B.F.L., o quella dell’angolo di campo o di diverse lunghezze d’onda.. La B.F.L. è la distanza lungo l’asse ottico dal vertice della superficie della lente posteriore o dello specchio primario al fuoco parassiale per un oggetto posto virtualmente all’infinito.

Si passa, quindi, all’esame  delle aberrazioni ottiche assiali ed extrassiali, la cui rilevanza è di assoluta preminenza sulla qualità dell’immagine finale fornita dall’obiettivo. Infatti, se si trascurano gli errori di fabbricazione o di assemblaggio, nonché gli effetti della diffrazione e della turbolenza atmosferica, sono proprio quei difetti che impediscono ad un sistema ottico di creare un’immagine perfetta, ossia un’immagine puntiforme di una sorgente luminosa puntiforme tanto sull’asse ottico, quanto a varie distanze dal medesimo.

6) Spherical Aberration + Coma  (O.S.C.) (Aberrazione sferica e coma)

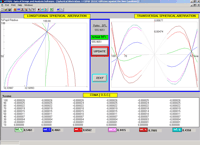
Un grafico mostra il comportamento dell’aberrazione sferica longitudinale ed uno di quella trasversale. L’aberrazione di sfericità si ha quando raggi luminosi paralleli all’asse ottico che entrano a diverse altezze  nell’obiettivo vanno a fuoco su punti differenti lungo l’asse ottico. Quelli più vicini a quest’ultimo si focalizzano ad una distanza maggiore dall’obiettivo, nel cosidetto fuoco parassiale, quelli più lontani in un punto più vicino all’obiettivo, nel fuoco marginale. L’aberrazione sferica longitudinale corrisponde alla differenza tra il fuoco marginale e quello parassiale, quella trasversale alla distanza tra l’asse ottico e i raggi marginali, misurata secondo la normale all’asse ottico sul fuoco parassiale.
L’aberrazione di coma sorge quando i raggi fuori asse paralleli che attraversano la lente o si riflettono su uno specchio vicino ai bordi intersecano la superficie del piano immagine in punti diversi rispetto a quelli prossimi al centro dell’obiettivo, con il risultato di avere per un oggetto luminoso puntiforme un’immagine a forma di ventaglio o di coda di cometa. Per essere libero dal coma un sistema ottico deve soddisfare la condizione dei seni di Abbe, la quale richiede che in un siffatto sistema ogni raggio in uscita di un fascio incidente di raggi paralleli all’asse rispetti la regola:

h/sin U¹ = C

dove (h) è l’altezza del raggio prima che entri nel sistema, (U¹) l’angolo tra il raggio e l’asse ottico diretto verso il piano focale e (C) una costante, che può essere considerata come la lunghezza focale effettiva di ciascuna zona della pupilla d’entrata. Noto il valore di (C), un altro importante parametro può essere calcolato ai fini dell’identificazione e determinazione del coma, cioè l’O.S.C. (Offense against the Sine Condition), che sarà pari alla differenza frazionale tra il valore assiale di (C)  e quello di (C) all’altezza (h):

O.S.C. = C (h) / C(o) – 1.

Questa formula è valida in assenza di aberrazione sferica e per oggetti posti all’infinito.

ATMOS riproduce questi valori in un grafico, ponendoli in relazione all’altezza del raggio. Ogni scostamento dall’ordinata indicherà la presenza e l’entità dell’aberrazione comatica. I dati relativi sono anche raccolti in una tabella.

7) Field Curvature (Sagittal, Tangential, Average) (Curvatura di campo)

Tale aberrazione, in genere, potrebbe essere trattata insieme con l’astigmatismo, dal momento che un obiettivo affetto da questo presenta sempre  due superfici focali, una o entrambe curve. Per oggetti fuori asse i raggi tangenziali vanno a fuoco sulla superficie focale tangenziale, quelli sagittali sulla superficie sagittale. Pertanto la curvatura di campo e l’astigmatismo potrebbero essere descritti come curvatura di campo tangenziale e sagittale. Oppure essi potrebbero venire interpretati come variazioni della B.F.L. ad angoli di campo e distanze fuori asse. Tra le due superfici focali ne esiste una terza mediale, ove l’immagine di una sorgente puntiforme assume l’aspetto di un discoide noto come circolo di minima confusione. In presenza di curvatura di campo l’immagine si forma su una superficie quasi sferica con la concavità verso l’obiettivo. A seconda del campo che l’utente desidera utilizzare, ATMOS fornisce risultati grafici e tabulari con parametri come la distanza dall’asse, le dimensioni delle superfici tangenziali e sagittali, il raggio di curvatura medio di campo della superficie di miglior fuoco.

8 ) Distortion (Distorsione)

La distorsione è l’aberrazione che mostra quanto e come un oggetto posto su una superficie piana normale all’asse ottico è riprodotto su una superficie d’immagine piana anch’essa perpendicolare all’asse ottico. Se la superficie dell’oggetto appare, ad esempio,  come una griglia rettilinea piana e la relativa immagine è riprodotta nello stesso modo, allora l’obiettivo è ortoscopico cioè privo di distorsione. Ma se le linee fuori asse della griglia appaiono curvate, allora siamo in presenza di distorsione, che può essere a cuscinetto positiva o a barilotto negativa. Essa è causata da una variazione nella scala trasversale dell’immagine o dell’ingrandimento in funzione dell’angolo di campo fuori asse o della distanza. ATMOS visualizza un diagramma con l’andamento dei due tipi di distorsione, insieme con una griglia in cui è rappresentata graficamente l’entità di questa aberrazione.

9) Lateral Color (Aberrazione cromatica laterale) e Chromatic Focal Shift

Se la lunghezza focale effettiva di una lente varia con la lunghezza d’onda, allora anche le dimensioni dell’immagine varieranno con la lunghezza d’onda. A seconda del segno di questa aberrazione, l’immagine nel rosso può risultare più grande o più piccola di quella nel blu. Questo difetto, noto come aberrazione cromatica laterale o differenza cromatica d’ingrandimento, può essere corretto con un metodo molto simile a quello usato per l’aberrazione cromatica longitudinale, ossia accoppiando vetri con differenti indici di dispersione. Rappresentata in un diagramma a macchie policromatico, questa aberrazione si rivelerebbe con degli sfasamenti trasversali nelle macchie d’immagine a varie lunghezze d’onda. ATMOS mostra in un apposito quadro lo spostamento del piano focale e della B.F.L. in relazione alla variazione cromatica.

Sempre nel menu Analysis troviamo un’altra serie di strumenti per valutare in maniera ancora più approfondita la struttura dell’immagine via via che il progetto ottico tende a definirsi, con concetti come l’interferenza, la diffrazione, i colori, il dominio delle frequenze che la semplice ottica geometrica non è in grado di spiegare. In questi casi la luce all’interno del sistema ottico viene considerata anche nella sua natura di onde elettromagnetiche o di pacchetti di fotoni.

10) Ray fan plot

Non sempre le informazioni ricavabili dall’analisi degli spot diagram sono sufficienti per diagnosticare certi tipi di aberrazioni ottiche e le loro entità, soprattutto per quelle che interessano talune zone della pupilla d’entrata che i raggi luminosi attraversano prima di giungere a formare i vari punti della spot d’immagine. A tale scopo risultano molto utili i grafici delle curve di intercettazione dei fasci di raggi luminosi (ray fan plot). Un fascio di raggi è un insieme di raggi provenienti da una sorgente luminosa puntiforme tutti disposti su un piano, che, di norma, è fatto passare per il centro della pupilla d’entrata con il fascio che si estende da un lato della pupilla all’altro. Quando un dato raggio nel fascio passa nella lente diretto verso la superficie dell’immagine, esso attraversa la pupilla d’entrata in una zona con una specifica altezza rispetto all’asse ottico. Nel momento in cui intercetta la superficie d’immagine, esso, di solito, cade a piccola distanza (mai pari a zero) dal raggio principale ( che è quello che parte da un bordo estremo della sorgente, passa per il centro dell’obiettivo, interseca l’asse ottico e prosegue fino al bordo del campo d’immagine). Questa distanza trasversale dal raggio principale è l’errore di altezza, cioè l’aberrazione, del raggio iniziale corrispondente alla zona di altezza della pupilla d’entrata già vista. Il relativo diagramma presenta in forma grafica questi errori di altezza del raggio sulla superficie d’immagine come una funzione della corrispondente altezza nella pupilla d’entrata. Gli errori sono considerati per due specifici fasci di raggi nel piano tangenziale e in quello sagittale, con raggi che intersecano la pupilla d’entrata lungo gli assi y e x, rispettivamente.

11) O.P.D. (Optical Path Difference)

Uno strumento analitico molto usato nell’Optical Design per calcolare e presentare le aberrazioni presenti nelle immagini è l’O.P.D. (Optical Path Difference). In pratica più raggi a varie altezze vengono seguiti attraverso il sistema ottico fin sul piano focale. Quindi si calcola la lunghezza totale del percorso del raggio espressa in unità di lunghezza d’onda. Nel caso in cui i raggi attraversino elementi a rifrazione le lunghezze di trasferimento sono moltiplicate per l’indice di rifrazione del vetro. Se il sistema è otticamente perfetto, le lunghezze del percorso di tutti i raggi saranno esattamente uguali, la luce, cioè, arriverà in fase; se, invece, i raggi arriveranno non in fase, ciò sarà il segno della presenza di aberrazioni ottiche. Quando la variazione della lunghezza del percorso non supera ¼ della lunghezza d’onda della luce utilizzata, il sistema è considerato “limitato dalla diffrazione”. E questo è, di solito, il normale livello di qualità presente negli strumenti astronomici amatoriali. ATMOS tratta le O.P.D. nella forma di ray fan plot, rappresentando graficamente gli errori O.P.D. del fronte d’onda nella pupilla d’uscita come funzione delle altezze di zona nella pupilla d’entrata. L’O.P.D. può essere considerata anche come la distanza lineare lungo un raggio tra l’attuale fronte d’onda aberrato nella pupilla d’uscita e quello ideale privo di aberrazioni.

12) Wavefront (Fronte d’onda)

Secondo la teoria dell’elettromagnetismo una sorgente luminosa emette nello spazio un flusso continuo e non limitato di onde elettromagnetiche che si propagano alla velocità della luce. Per ogni istante temporale la luce di una data lunghezza d’onda emessa da una sorgente puntiforme è in fase. Pertanto su superfici con costante tempo di percorrenza della luce proveniente da una sorgente puntiforme tutte le onde sono in fase, ossia le onde monocromatiche da punto a punto su queste superfici sono spazialmente coerenti. Queste superfici di fase costante sono dette fronti d’onda; se la sorgente è immersa in un mezzo con indice di rifrazione costante, allora i fronti d’onda hanno forma curva sferica con il centro di curvatura sulla sorgente ed essi appaiono come superfici normali ai raggi luminosi. Un sistema ottico privo di aberrazioni produce un flusso di fronti d’onda sferici convergenti in ciascun punto dell’immagine che viene a formarsi sul piano focale. ATMOS considera il fronte d’onda a proposito della valutazione degli effetti dei corrispondenti errori O.P.D., fornendone una mappa con rappresentazione tridimensionale della superficie del fronte d’onda con possibilità di rotazione negli assi x,y,z. Queste irregolarità sono errori di distanza o di percorso misurati longitudinalmente lungo i raggi, intese come separazioni fra il reale fronte d’onda aberrato nella pupilla d’uscita e quello sferico esente da aberrazioni detto anche sfera di riferimento che ha il centro di curvatura sulla superficie di immagine e il vertice su quello della superficie della pupilla d’uscita. Le aberrazioni O.P.D. del fronte d’onda possono essere specificate in vari modi, che troviamo chiari in ATMOS:

1. range totale dell’O.P.D. peak-to-valley (dallo scostamento estremo positivo a quello estremo negativo rispetto al fronte d’onda di riferimento);
2. massimo scostamento del valore assoluto del fronte d’onda reale da quello di riferimento;
3. R.M.S. scostamento del fronte d’onda dalla sfera di riferimento valutato sull’intera pupilla d’uscita;
4. scostamento del fronte d’onda reale da quello di riferimento espresso con i polinomi di Zernike;
5. Strehl ratio.

Per ottenere immagini limitate dalla diffrazione non è necessario che un obiettivo abbia prestazioni geometriche assolutamente perfette, cioè che sia del tutto esente da aberrazioni ottiche. Infatti, se le dimensioni della macchia in un relativo diagramma è molto più piccola del disco di Airy, la diffrazione supera le aberrazioni geometriche e le immagini di oggetti puntiformi sono praticamente indistinguibili da una perfetta figura di Airy. Allo stesso modo, se gli errori O.P.D. nella pupilla d’uscita sono molto più piccoli della lunghezza d’onda della luce, le aberrazioni saranno di nuovo indistinguibili. Se un obiettivo è privo di aberrazioni, allora la corrispondente figura di Airy è la più compatta e luminosa immagine che esso è in grado di produrre e l’irradianza al centro del disco di Airy è la massima possibile, mentre, in presenza di aberrazioni, la luce viene sparpagliata entro una certa area e il picco di irradianza dell’immagine aberrata (P.S.F.) appare sempre ridotto. Il rapporto fra questo picco e quello della relativa immagine (P.S.F.) libera da aberrazioni è detto Strehl ratio. Per comuni immagini limitate dalla diffrazione lo scostamento di questo rapporto dalla condizione ideale ( 1% o 100%) dipende dal tipo di strumento e dalle applicazioni pratiche a cui è destinato: valori di 80% – 90% sono più che accettabili. Se vi sono elementi ostruttivi nel percorso ottico o problemi di vignettatura meccanica che comportano un calo della quantità effettiva di luce trasmessa sul piano focale, di questi elementi si tiene conto nel calcolo di entrambi i termini dello Strehl ratio.

13) Interferogram (interferogramma)

Questa funzione è, in sostanza, una differente rappresentazione del Wavefront. La misura dell’O.P.D. per frangia, che di default vale 0,5 o mezza lunghezza d’onda, ci dice che nell’interferogramma visualizzato la distanza tra una frangia e l’altra corrisponderà ad un salto di ½ d’onda. Inoltre la possibilità di introdurre una certa inclinazione nelle direzioni X e Y consente di vedere più frange contemporaneamente, così da valutare la correzione del sistema a seconda della loro deformazione. In definitiva è una buona simulazione delle prestazioni dell’obiettivo da confrontare con gli analoghi sistemi di controllo che nei laboratori ottici vengono usati per testare la qualità dell’obiettivo durante le fasi conclusive della lavorazione.

14) E.E.P. (Encircled Energy Plot)

E’ un calcolo geometrico effettuato sullo spot-diagram. Partendo da un cerchio centrato sul raggio principale o sul centroide, vengono contati quanti sono i raggi non vignettati, e quindi l’energia, che cadono entro cerchietti di diametro crescente.
In ATMOS troviamo un grafico che mostra in ordinata la distribuzione percentuale dell’energia luminosa in funzione della distanza da uno dei punti di riferimento sull’ascissa, affiancato da un tabella dei relativi valori numerici.

15) P.S.F. (Point Spread Function)

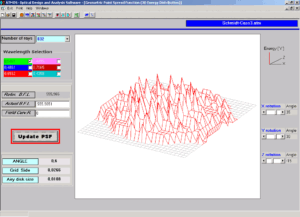
Il concetto di P.S.F. (Point Spread Function) è utilizzato per spiegare l’impossibilità di ottenere di una sorgente luminosa puntiforme una corrispondente immagine puntiforme perfetta da un punto di vista matematico. La P.S.F. fornisce la corretta distribuzione fisica della luce nell’immagine di un oggetto puntiforme considerando gli effetti delle aberrazioni geometriche e della diffrazione, mentre non si tiene conto dei disallineamenti meccanici, della turbolenza atmosferica e degli errori di lavorazione dell’obiettivo che possono riguardare la curvatura e la figura delle superfici, gli indici di rifrazione e dispersione cromatica, l’omogeneità dell’indice di rifrazione, lo spessore degli elementi ottici o della spaziatura in aria, lo sfasamento assiale, il decentramento trasversale e l’inclinazione delle superfici ottiche.

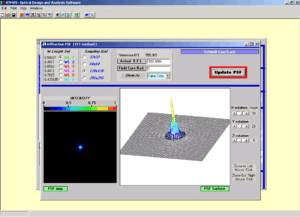
I due principali tipi di P.S.F., prodotti, cioè, dalle aberrazioni geometriche o dalla diffrazione, sono molto utili al progettista perché forniscono una misura della miglior qualità d’immagine che un certo progetto teorico è in grado di assicurare. ATMOS calcola entrambe le P.S.F., mostrando i risultati in forma di mappa bidimensionale di distribuzione dell’intensità dell’energia luminosa e di grafico tridimensionale della superficie del sistema ottico, utilizzando il metodo delle F.F.T. (Fast Fourier Transform), un tipo di calcolo applicato nel campo del dominio delle frequenze spaziali.

Una tipica immagine di P.S.F. rivela un largo picco centrale circondato da una serie di anelli luminosi concentrici di irradianza decrescente verso l’esterno, alternati da anelli scuri che rappresentano i luoghi in cui l’irradianza ha valore zero, sempre a specifiche distanze dal centro. Questa distribuzione di luce limitata dalla diffrazione è detta anche pattern di Airy e il picco al suo centro altro non è che il disco di Airy. E’ chiaro, allora, che quanto più quel picco apparirà stretto e alto, tanto più intensa sarà la concentrazione di luce, a tutto vantaggio di una migliore puntiformità e brillantezza delle immagini stellari, e quanto più regolari e morbidi risulteranno gli anelli concentrici, tanto più l’immagine finale diventerà dettagliata e precisa.

16) M.T.F. (Modulation Transfer Function)

L’ M.T.F. (Modulation Transfer Function) fornisce una misura diretta di come e quanto i vari dettagli a diverso indice di contrasto presenti in un oggetto di riferimento sono contenuti nella corrispondente immagine riprodotta da un sistema ottico sul suo piano focale. E’ nota anche come risposta in frequenza spaziale o risposta dell’onda sinusoidale ed ha valori compresi tra 0% e 100%.  La modulazione (o contrasto)  (M) ad una data frequenza (v) è data dal rapporto:

M(v) = Imax – Imin / Imax + Imin

in cui (I) indica la radianza o intensità luminosa massima e minima. Per la misura del trasferimento di contrasto si utilizza un reticolo composto da linee chiare e scure equidistanti di dimensioni via via più ridotte da porre davanti al sistema ottico. Il rapporto fra il contrasto dell’immagine risultante (Ci) e quello dell’oggetto ripreso (reticolo) (Co) è detto coefficiente di trasferimento del contrasto (CT):

CT = Ci /Co

La relazione tra questo coefficiente e il numero di linee/mm presenti nell’immagine è riproducibile in un grafico della funzione di trasferimento della modulazione (M.T.F.) o di funzione di trasferimento del contrasto (C.T.F.). Per un sistema ottico perfetto si avrà una curva quasi del tutto rettilinea con un piede lievemente degradante. Le curve M.T.F consentono di valutare l’ampiezza delle aberrazioni dell’immagine e degli effetti della diffrazione di un sistema ottico non corretto rispetto al profilo ideale di uno perfetto. Le curve di quello imperfetto non coincideranno quasi mai con quelle di uno schema ideale e dall’esame di questo scostamento si potrà analizzare quanto e per quale causa il contrasto dell’immagine creata dal sistema ottico progettato sarà più basso se confrontato con l’andamento teorico. Ciò può accadere per via della presenza di aberrazioni geometriche oppure per difetti nella lavorazione delle superfici dell’obiettivo o ancora per l’interposizione di elementi ostruttivi lungo il percorso ottico che modifichino la figura di Airy o, infine, per riflessi interni al tubo ottico o raggi parassiti esterni non adeguatamente schermati da un efficace sistema di diaframmi. Attraverso l’analisi delle curve M.T.F. è possibile, quindi, ottimizzare i parametri dell’ottica progettata in modo che fornisca le migliori prestazioni teoriche a seconda del tipo di applicazioni a cui andrà destinata: diametro più grande possibile per sfruttare al meglio la capacità di raccolta di luce e il potere di risoluzione, ostruzione contenuta, riduzione degli errori di fabbricazione, schemi ottici con aberrazioni assiali ed extrassiali minime e controllabili, superfici ottiche rivestite da protezioni antiriflessi per assicurare il più alto trasferimento del contrasto nell’immagine finale. Il tutto per cercare di ottenere curve M.T.F. reali quanto più coincidenti con quelle ideali. ATMOS analizza queste curve sotto il profilo geometrico e della diffrazione, ponendole entrambe in relazione alle variazioni del fuoco e all’ampiezza del campo di visione, che spazia dallo 0%  (coincidenza con l’asse ottico), al 70% e al 100%, sia nel piano tangenziale (curva rossa) che in quello sagittale (curva blu).

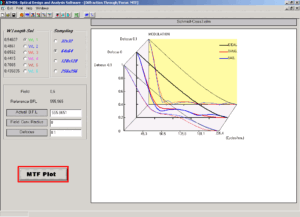
Il menu Analysis si chiude con le tabelle relative al tracciamento dei raggi reali (Real Rays) e al calcolo parassiale (Parassial Calculation), quest’ultimo articolato in un setup, nella raccolta dei dati per il raytrace, nei coefficienti di Seidel per le aberrazioni ottiche trasversali e longitudinali.

Troviamo, poi, un grafico che mette in evidenza la percentuale di vignettatura presente nel sistema ottico (Vignetting Plot), ossia la porzione di campo non perfettamente illuminato dell’obiettivo a causa di un inesatto dimensionamento delle componenti ottiche o meccaniche ( ad es. una lastra correttrice di diametro uguale a quello dello specchio primario in una camera di Schmidt).

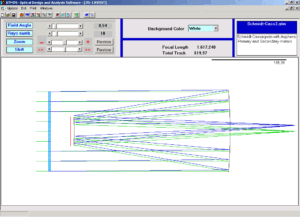
Infine lo schema ottico dello strumento progettato prende forma attraverso il Layout 2D o 3D, in cui ATMOS disegna su un piano bidimensionale o tridimensionale la struttura, il numero degli elementi ottici in forma lineare o solida, il percorso seguito da una quantità variabile di raggi luminosi all’interno dello schema stesso.

Nel menu (Telescope Predesign) sono contenuti una serie di quadri preimpostati relativi a molte delle principali configurazioni ottiche per uso astronomico: riflettore Newton, riflettori a due specchi Cassegrain, Gregory e Coudé-Schwarzschild, Camera Schmidt e Wright ad uno specchio, Catadiottrici Schmidt Cassegrain in versione compatta con ottiche sferiche e asferiche e in versione non compatta o monocentrica, Maksutov ad uno specchio e Maksutov Cassegrain a due specchi, Lurie Houghton ad uno specchio sferico o asferico e Houghton Cassegrain, ed infine gli obiettivi a rifrazione doppietti e tripletti, acromatici e apocromatici.

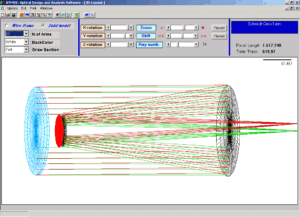
Per ogni sistema  prescelto ATMOS offre lo schema della combinazione ottica con alcuni importanti parametri geometrici e le distanze degli elementi ottici. Si richiede l’inserimento di specifici dati come la lunghezza focale effettiva, il diametro dell’eventuale correttore, la distanza dal vertice del primario al piano focale, il diametro lineare del campo non vignettato che si desidera, le lunghezze d’onda selezionate, il tipo di vetro ( con relativa automatica determinazione dell’indice di rifrazione), lo spessore dell’eventuale correttore, la posizione della zona neutra.

Dopo aver fornito queste indicazioni tecniche ATMOS provvede a calcolare il raggio di curvatura del primario, del secondario e del correttore, la distanza primario-secondario, il diametro del primario e del secondario, l’ingrandimento di quest’ultimo, soprattutto nei sistemi Cassegrain, la B.F.L., la percentuale di ostruzione lineare, il rapporto focale, la distanza primario-correttore nei sistemi catadiottrici, la potenza del correttore.
Completano gli strumenti a disposizione del progettista i diagrammi dei vetri ottici, una serie di grafici contenuti in un apposito menu (Glass Diagram) relativi alle caratteristiche di un gran quantità di vetri prodotti da Schott, Ohara, Corning e Hoya. Di essi si prendono in considerazione gli indici di rifrazione e i valori della dispersione cromatica (numeri di Abbe). I primi sono dati per le linee d (a 587,56 nm) ed e (a 546,07 nm), mentre i secondi si ottengono dalla differenza tra gli indici di rifrazione per le linee F (a 486,13 nm) e C (a 656,27 nm) e per le linee F1 (a 479.99 nm) e C1 ( a 643,85 nm) rispettivamente. I vetri sono selezionabili sia puntando il  mouse all’interno dei suddetti grafici, sia da apposite tabelle comprendenti i cataloghi dei prodotti con la specificazione degli indici di rifrazione per tutte le principali linee e lunghezze d’onda spettrali, i numeri di Abbe ed i valori di dispersione relativa parziale.

Il lavoro progettuale non può dirsi concluso se non è rifinito con l’ottimizzazione del sistema ottico. Questo processo, che troviamo trattato in ATMOS nel menu (Tools- Optimization), richiede una valutazione complessiva dell’esattezza dei metodi via via applicati, per giungere attraverso varie iterazioni alle migliori prestazioni. Naturalmente il software deve essere in grado di identificare questo obiettivo finale, deve, cioè, disporre di una misura di qualità che viene chiamata anche funzione di merito o funzione di errore. Nel caso di un sistema ottico perfetto il suo valore sarebbe pari a zero, ma la presenza di aberrazioni residue aumentano sempre i valori reali. Per mezzo dell’ottimizzazione il progettista cerca di ridurre il valore della funzione di merito il più possibile, approssimandola a zero, agendo su tutti i parametri ottici, parassiali, gaussiani, meccanici, nonché sulle aberrazioni che incidono sulla definizione e distorsione dell’immagine. I singoli elementi della funzione di merito sono detti operandi di ottimizzazione, in pratica delle funzioni di raggi, fronti d’onda o altre proprietà costruttive dell’obiettivo sui quali si desidera intervenire. Il controllo sugli operandi viene effettuato con il metodo dei minimi quadrati, il quale permette di regolare i parametri ottici in modo che la somma dei quadrati pesati degli errori rilevati per tutti gli operandi nella funzione di merito sia la più piccola possibile.

Sempre in (Tools) troviamo le funzioni (Best Focus) che fornisce la posizione del punto focale ove l’immagine è più corretta sull’asse ottico R.M.S. e a pieno campo in luce mono e policromatica; (Scale factor) e (New Focal Lenght) necessarie per calcolare un nuovo sistema ottico del quale si è semplicemente ridotta la scala o variata la focale; (Sagitta Table) (Element Volume) per avere i dati della sagitta e di volume del sistema ottico; (Aberrations Allowances) per disporre dei dati numerici riferiti alle tolleranze di aberrazione, assumendo come parametro di riferimento il limite di Rayleigh del quarto d’onda; (System Data Report), il riassunto finale tabulare dei dati ottenuti.

ATMOS è, dunque, un software di Optical Design molto completo e indispensabile per i progettisti di ottica ma che non mancherà di entusiasmare anche gli astrofili, gli autocostruttori e gli appassionati  di telescopi ed altri accessori ottici, che desiderino comprendere a fondo il funzionamento dei loro semplici e meravigliosi strumenti e migliorarne le prestazioni. Unici nei rilevati nella versione 7.0 sono la mancanza di un manuale o di un help in linea più ricco di informazioni e spiegazioni delle varie funzioni, alcune delle quali potrebbero risultare di non facile comprensione e applicazione, nonché della possibilità di salvare i quadri di lavoro nei più comuni formati grafici.