E’ una metafora bizzarra? Non troppo, come vedremo! Sta per iniziare un periodo di sei anni in cui la Luna incontrerà le Pleiadi ogni mese, dando luogo ad un ciclo di occultazioni, delle quali poco più di una ventina osservabili dall’Italia (la prima sarà di Atlante, il 20/10/2005, visibile dalla Sicilia). Passata questa ondata, dopo il febbraio 2011, occorrerà aspettare fino al 2023 per averne una nuova, anch’essa della durata di sei anni. Ma le Pleiadi sono in fondo una scusa per porci una domanda: come mai questa attesa? Ovvero, come mai la Luna, nel suo moto di rivoluzione, non segue sempre lo stesso percorso, proiettandosi sempre nelle stesse posizioni del cielo?
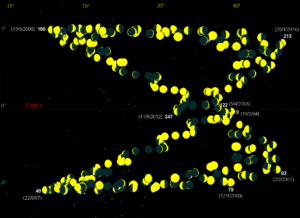
Ebbene, di tutti gli oggetti del Sistema Solare, la nostra Luna è proprio quello il cui moto è più ondivago e più difficile da descrivere matematicamente. Non dico che si muova come un marinaio ubriaco, ma almeno un po’ alticcia lo è, basta guardare la Figura 1. Questa rappresenta una regione della volta celeste attorno alle Pleiadi, con le posizioni occupate dalla Luna “fotografate” ad intervalli costanti di 27.3215 giorni (corrispondenti al periodo medio siderale di rivoluzione). Per ricavare matematicamente quelle ali di farfalla, anche se solo con la precisione di un mezzo minuto d’arco, sarebbero necessari centinaia di termini correttivi da aggiungere a quelli che descrivono una semplice orbita Kepleriana. E’ chiaro che, usando un modello e uno strumento di calcolo che tengano conto di tutte le perturbazioni (in massima parte dovute all’attrazione gravitazionale del Sole), la posizione della Luna in ogni istante può essere ricavata con precisione senza problemi, ma la nostra ambizione di visualizzare e comprendere concettualmente, anche se in maniera approssimativa, il percorso celeste del nostro satellite, affoga così nel guazzabuglio della complessità matematica. In questo mare agitato, è possibile trovare non dico una scialuppa, ma almeno un salvagente?
Proviamo a fare una semplificazione, tagliando via il grosso del problema e tenendocene appena un pezzetto. Interessiamoci solo del percorso seguito dalla Luna sulla volta celeste, senza preoccuparci del momento in cui si troverà in ciascun punto di quel percorso, né della distanza da noi. Abbiamo così rimosso la variabile tempo.
Immaginiamo ora di orientare la sfera celeste, ruotandola in modo che il piano “orizzontale” coincida con il piano dell’eclittica.
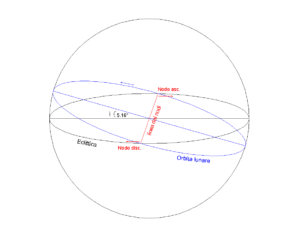
Il percorso della Luna sulla sfera sarà un cerchio massimo che interseca il nostro piano “orizzontale” lungo una retta (chiamata linea dei nodi), formando un angolo i (chiamato inclinazione), che è in media 5.16° (Figura 2). Immaginiamo ora di aprire la sfera come la buccia di un’arancia, dopo averne rimosse le calotte superiore e inferiore, e di distendere poi su di un piano ciò che rimane. La superficie della corona sferica si trasforma così in un rettangolo, il cui asse orizzontale indicherà la longitudine eclittica e quello verticale la latitudine eclittica (Figura 3).
Ed ecco che in questa mappa il percorso della Luna si è trasformato in una curva che chi mastica un po’ di trigonometria riconoscerà come una sinusoide (a rigore non lo è, ma ci si avvicina quasi esattamente). I “nodi” della sinusoide, cioè i punti in cui questa interseca l’asse orizzontale, corrispondono proprio ai nodi ascendente e discendente dell’orbita (vedi Figura 2), mentre l’ampiezza è uguale alla inclinazione i (5.16°). Ad ogni rivoluzione, della durata media di 27.3215 giorni, la Luna percorrerà la curva da destra verso sinistra… ma non sarà sempre la stessa sinusoide. Già, perché il principale effetto dell’attrazione solare è di far ruotare la linea dei nodi nel piano dell’eclittica in direzione opposta al moto della Luna, con un giro completo ogni 18.61 anni. A causa di questa “precessione dei nodi” la nostra curva si sposta verso destra nel piano orizzontale in media di circa 1.45° ad ogni rivoluzione, “uscendo” da destra e “rientrando” da sinistra, fino a tornare nella posizione originale dopo 18.61 anni. Volendo essere un po’ più precisi, c’è da dire che l’inclinazione non è costante, e la precessione dei nodi non è uniforme, ma entrambe subiscono delle piccole oscillazioni attorno al loro valore medio, introducendo così un po’ di imprecisione nel nostro modello di sinusoide mobile, di cui si terrà però debito conto.
Siamo ora quasi del tutto equipaggiati con uno strumento adatto a descrivere i cicli di occultazioni. Ci manca solo un’altra considerazione. Quanto detto fin’ora vale per una Luna puntiforme, che sia vista dal centro della Terra. La Luna ha invece un raggio apparente (cioè l’angolo visuale che sottende nel cielo) di 0.26 ± 0.02° (a seconda della distanza). Inoltre noi non la osserviamo dal centro della Terra, ma da un punto della sua superficie che, a seconda della località e del moto diurno del nostro pianeta, può “vedere” la Luna in una posizione che differisce da quella “geocentrica” fino a 1° (vedi Figura 4).
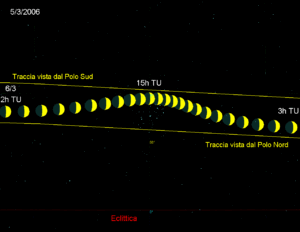
Ne consegue che, perché in qualche punto della Terra sia visibile l’occultazione di una data stella, basta che la Luna passi entro 1.2° dalla stessa (± 0.1° a seconda della distanza della Luna). Possiamo allora concludere che una occultazione si può verificare solo se la sinusoide di Figura 2 passa a meno di 1.2° dalla stella, con un margine massimo di incertezza di ± 0.25°, che tiene conto sia dell’intervallo entro il quale può variare la distanza Terra-Luna, sia di quello entro cui può variare l’inclinazione dell’orbita lunare.
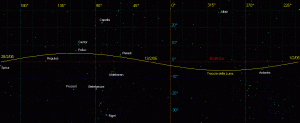
Il gioco è fatto! Possiamo tornare alle Pleiadi, e per esse riferirci alla stella più brillante dell’ammasso, η Tauri, Alcyone. Supponiamo di essere al Capodanno del 2005: la longitudine media λ della Luna è 165.0°. Con l’aiuto di un software grafico, o anche solo di una matita, un foglio di carta millimetrata e una calcolatrice tascabile, possiamo disegnare la sinusoide di Figura 5. Per farlo ci basta conoscere un solo dato: la longitudine media del nodo ascendente all’epoca considerata, (28.3° al 1/1/05), mentre l’ampiezza la conosciamo già, perché è uguale alla inclinazione media, cioè 5.16°. La Luna percorrerà la sinusoide da destra verso sinistra, partendo dalla longitudine di 165°, alla velocità media di 13.1764° al giorno, ma potrà essere in anticipo o in ritardo rispetto alla posizione “media” fino a 8°, corrispondenti a circa 0.6 giorni. Sopra e sotto la sinusoide ne sono tracciate altre due, sfalsate di ± 1.2° in verticale rispetto alla prima, che delimitano la zona del grafico, entro la quale deve trovarsi una stella perché sia osservabile (da qualche punto sulla Terra) una occultazione.
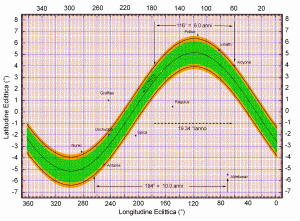
Il contorno di questa fascia non è netto, ma è sfumato nelle zone arancioni della figura, corrispondenti al margine di incertezza visto prima di ± 0.25° in latitudine. Nel grafico sono state inserite, ricavandole da un catalogo, le posizioni di alcune stelle brillanti situate in vicinanza dell’eclittica. Alcyone viene a trovarsi all’esterno della sinusoide superiore, distante da questa circa 2° di longitudine, ma entro la “zona arancione”. Secondo il nostro strumento grafico, ciò significa che in Gennaio una occultazione potrebbe essere possibile (anche se non molto probabile): quando? Se la longitudine (media) di partenza è 165°, la Luna dovrà percorrere 255° (“uscendo” da sinistra e “rientrando” da destra), e, alla velocità media di 13.1764 °/giorno, raggiungerà le Pleiadi dopo 255/13.1764 = 19.35 ± 0.6 giorni, cioè il 19 o il 20 gennaio. Di fatto la Luna sarà (o è stata) in congiunzione con le Pleiadi alle 22 TU del 19 gennaio, ma senza dare occultazioni. Ora immaginiamo di traslare le curve pian piano verso destra nel movimento della precessione dei nodi. Quattro settimane dopo si sono spostate di 1.45°, e Alcyone tocca la sinusoide superiore: una occultazione diventa abbastanza probabile, ma il punto di vista deve trovarsi abbondantemente al di sotto dell’eclittica, quindi nell’emisfero meridionale. Di fatto ci sarà, il 16 Febbraio, la prima occultazione, visibile nel Pacifico meridionale. Nei mesi successivi la nostra “onda”, continuando a spostarsi verso destra in media di 1.45° ad ogni periodo lunare, “sommergerà” Alcione, e ci sarà così una occultazione ad ogni passaggio della Luna. Continuando lo spostamento, la stella rimarrà costantemente entro la fascia di visibilità delle occultazioni, riemergendone solo dopo uno scorrimento complessivo di 116°.
Quanto tempo impiega la sinusoide a scorrere di 116° ? Se ci vogliono 18.61 anni a fare tutto il giro di 360°, il tempo necessario sarà 18.61•116/360 = 6.0 anni dal Capodanno del 2005. Per avere poi la occultazione successiva, occorrerà ritornare pressappoco nelle condizioni della prima, il che avverrà dopo 18.61 anni dal febbraio del 2005, quindi nel settembre del 2023.
Ora, la Tabella 1 riporta una selezione delle occultazioni (visibili e non) di Alcione nel prossimo e nel successivo ciclo, calcolate con il programma SOLEX (vedi Coelum no. 64) e tutta la precisione possibile. L’ultima del prossimo ciclo (quasi invisibile nella luce crepuscolare a Sud della Terra del Fuoco, bassissima sull’orizzonte) vi sarà il 19/12/2010: mancheranno pochi giorni a 6.0 anni! La prima del successivo ciclo (visibile nel Mare Antartico a Sud dell’Australia) si avrà il 5 settembre 2023!
Direi che il salvagente per non affogare con la mente nelle onde del moto lunare lo abbiamo trovato! Anzi, forse è anche qualcosa di più, dato che la variabile tempo, uscita dalla porta, è poi in parte rientrata dalla finestra… La nostra mappa eclittica di Figura 2, insieme a un righello e a una matita, ci può infatti servire a prevedere se e quando sarà possibile una occultazione lunare di una qualsiasi stella, e quanto durerà il ciclo di occultazioni della stessa. Ci può mostrare ad esempio che una stella molto vicina all’eclittica (es. Regulus) non darà un solo e prolungato ciclo di occultazioni in un periodo di 18.6 anni, ma due più brevi, o che la prossima occultazione di Aldebaran ci sarà fra 10 anni… ma non vorrei dilungarmi troppo, e non vorrei togliere a chi fosse interessato la soddisfazione di provare da solo! Naturalmente le previsioni sono solo approssimative, e una parte delle occultazioni potrebbe avvenire di giorno e perciò non essere visibile. Questo purtroppo le nostre sinusoidi non ce lo possono dire, come pure non possono dirci esattamente quando e dove sarà osservabile ciascuna occultazione. Ma in fondo un semplice salvagente (o un canottino) servono per restare a galla, non per doppiare Capo Horn!
Tabella 1. Selezione delle occultazioni di Alcione nei prossimi due cicli (sono dati i tempi della minima distanza geocentrica). Quelle marcate da un asterisco sono visibili dal territorio italiano. β è la latitudine della Luna.
No. |
Data |
Ora (TDT) |
Dmin (°) |
β (°) |
| 1 | 2005/02/16 | 05:35 | 1.084 | 2.969 |
| 2 | 2005/03/15 | 13:59 | 0.897 | 3.157 |
| 3 | 2005/04/11 | 23:09 | 0.844 | 3.209 |
| 4 | 2005/05/09 | 07:43 | 0.875 | 3.178 |
| 5 | 2005/06/05 | 14:50 | 0.877 | 3.176 |
| ………. | ||||
| 22* | 2006/09/12 | 21:06 | 0.739 | 4.789 |
| 23 | 2006/10/10 | 06:13 | 0.707 | 4.757 |
| 24 | 2006/11/06 | 16:54 | 0.621 | 4.672 |
| 25* | 2006/12/04 | 03:13 | 0.605 | 4.655 |
| ………. | ||||
| 51* | 2008/11/13 | 20:26 | 0.736 | 4.787 |
| ………. | ||||
| 60* | 2009/07/18 | 02:57 | 0.540 | 4.590 |
| ………. | ||||
| 76 | 2010/09/28 | 06:20 | 1.012 | 3.041 |
| 77 | 2010/10/25 | 11:56 | 1.183 | 2.871 |
| 78 | 2010/12/19 | 03:45 | 1.198 | 2.856 |
| 79 | 2023/09/05 | 20:52 | 1.113 | 2.941 |
| 80 | 2023/10/03 | 05:47 | 0.991 | 3.062 |
| 81 | 2023/10/30 | 15:51 | 0.988 | 3.065 |
| ………. | ||||
| 92* | 2024/08/26 | 03:39 | 0.125 | 4.176 |
| ………. | ||||
| 100* | 2025/04/01 | 20:57 | 0.644 | 4.695 |
| 101 | 2025/04/29 | 07:05 | 0.568 | 4.618 |
| 102 | 2025/05/26 | 17:53 | 0.535 | 4.585 |
| 103* | 2025/06/23 | 03:29 | 0.612 | 4.662 |
| ………. | ||||
| 135* | 2027/11/14 | 18:58 | 0.497 | 4.547 |
| 136 | 2027/12/12 | 04:38 | 0.527 | 4.577 |
| 137 | 2028/01/08 | 15:11 | 0.609 | 4.659 |
| 138* | 2028/02/05 | 00:32 | 0.610 | 4.660 |
| ………. | ||||
| 155 | 2029/05/14 | 04:02 | 1.104 | 2.949 |
| 156 | 2029/06/10 | 10:52 | 1.082 | 2.971 |
| 157 | 2029/07/07 | 18:44 | 1.072 | 2.982 |
Nota: Le occultazioni più interessanti per l’osservazione sono quelle che si verificano dalla metà di Febbraio alla metà di Aprile, perché in questo periodo la posizione del Sole è tale che la Luna nelle Pleiadi, si trova entro il quarto crescente, e quindi il primo contatto con la stella avviene sul lembo oscuro e non su quello illuminato.



















