Indice dei contenuti
Introduzione
Come tutti sappiamo, la materia che ci circonda è formata da atomi, costituiti a loro volta da un nucleo centrale fatto da protoni e neutroni, e dagli elettroni che gli gravitano vorticosamente intorno.
Un po’ meno noto è forse il fatto che un atomo è quasi completamente vuoto; il nucleo, infatti, ha un diametro che è circa un centomillesimo di quello dell’atomo che lo ospita, mentre gli elettroni sono addirittura considerati puntiformi. Quasi completamente vuoto, quindi, allora perché non si può schiacciare un po’?
Normalmente, stando alle nostre esperienze quotidiane, un gas (che è fatto da atomi o da molecole libere tra loro) può essere compresso facilmente in un volume un po’ più piccolo aumentandone semplicemente la pressione, esattamente come quando gonfiamo una ruota di una bicicletta, con il risultato che gli atomi del gas si avvicinano un po’ tra di loro, di pari passo cresce anche la densità.
Un’operazione però che non si può eseguire ad oltranza; succederà infatti prima o poi che, come in un liquido o in un solido, gli atomi saranno vicini a tal punto che i loro orbitali atomici arriveranno a toccarsi, inutile continuare a “pressare”, non si andrà oltre. O quasi.
Al centro del nucleo terrestre che è composto quasi esclusivamente di ferro e dove vigono pressioni elevatissime che arrivano a 360 GPa (circa 3,5 milioni di atmosfere), la densità sale a circa 13 g/cm3 contro il classico 7,8 g/cm3 in condizioni normali; ancora più estremo è il centro del nostro Sole, dove, grazie ad una pressione di oltre 230 miliardi di atmosfere, la densità tocca picchi di circa 150 g/cm3, ovvero circa 20 volte la densità dell’acciaio.
 Nane Bianche
Nane Bianche
Ma questo è solo l’inizio.
Una volta che il nostro Sole avrà terminato il suo combustibile nucleare, la materia che lo compone, non più sorretta dall’energia prodotta dalle reazioni nucleari, collasserà su se stessa, aumentando sempre di più la sua densità.
In condizioni normali la pressione di un gas ideale è proporzionale alla sua temperatura e alla sua densità; superando però una densità di 105 g/cm3, le distanze interatomiche sono tali che le nubi elettroniche dei vari atomi sono portate a compenetrarsi a vicenda e, viste le temperature in gioco (circa cento milioni di gradi Kelvin) sono completamente ionizzati, formando così un gas di nuclei ed elettroni; raggiunto il milione di gr/cm3 (1.000 kg/cm3), la pressione del gas è a un livello tale che essa risulta indipendente dalla temperatura e non segue più le leggi classiche, bensì viene regolato in base alla fisica della materia condensata, in cui il maggior contributo alla pressione è dato dal principio di esclusione di Pauli (vedi Coelum Astronomia n°258 pag.92).
Questa sostanza che abbiamo ottenuto, un gas di Fermi relativistico, è chiamata ‘gas degenere di elettroni’, si comporta non differentemente da un gas di elettroni allo zero assoluto e la sua densità media è dell’ordine delle tonnellate per centimetro cubo (un elefante adulto pesa tre tonnellate, pensate a condensarlo in una zolletta di zucchero).
Ma questo gas degenere è ancora relativamente comprimibile: aumentando la pressione, se la massa della stella di partenza è sufficiente, gli elettroni acquisteranno sempre maggiore velocità e la densità salirà di conseguenza; ne deriva che una nana bianca, dalle dimensioni tipicamente paragonabili a quelle della Terra, sarà stranamente più piccola nelle stelle con maggiore massa, grazie alla pressione finale più elevata.
Questo però vale fino a che la massa della stella rientra entro un certo valore, chiamato “limite di Chandrasekhar”; per i più arditi, questo valore si ottiene applicando la formula
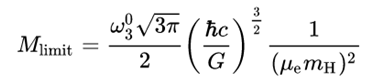
dove ħ è la Costante di Planck ridotta, c è la velocità della luce nel vuoto, G è la Costante Gravitazionale, μe è la massa molecolare media per elettrone che dipende dalla composizione chimica della stella, mH è la massa dell’atomo di idrogeno e ω03 (≈ 2.0182) è una costante connessa alla soluzione dell’equazione di Lane-Emden (fonte: Wikipedia), e vale 1,44 masse solari.

una stella di neutroni vicino al suo centro (Autore: Space Telescope
Science Institute Office of Public Outreach; Ringraziamenti:
NASA, ESA, CSA, STScI, D. Milisavljevic (Purdue University), T.
Temim (Princeton University), I. De Looze (University of Gent).
Stelle di Neutroni
Superato questo valore, la densità cresce sempre più e con essa la velocità degli elettroni, che giunge ad essere vicina a quella della luce; a questo punto, gli elettroni urtano così violentemente i protoni dei nuclei da fondersi con essi, dando origine ai neutroni.
È nata una stella di neutroni.
In realtà il processo è più complesso e comunque non omogeneo; un neutrone, nel vuoto e in quiete, ha una vita media di circa 15 minuti, e decade in un protone, un elettrone e un antineutrino:
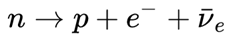
l’energia rilasciata da questa reazione, distribuita come energia cinetica nelle tre particelle ottenute, è di 0,782±0,013 MeV, e questo significa che, per mantenere stabile un neutrone indefinitamente, è necessario rendere questo decadimento non più conveniente dal punto di vista energetico.
Ora, un aumento della densità del gas degenere comporta un innalzamento del livello di Fermi e quindi un corrispondente aumento dell’energia cinetica di ogni singola particella del gas, fino a che questo raggiunge la soglia necessaria a impedire quanto sopra e addirittura a ottenere il processo inverso, ovvero il processo chiamato neutronizzazione:
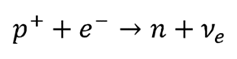
dove alcuni elettroni liberi vengono catturati dai protoni presenti nei nuclei, rilasciando neutrini che sfuggono dalla stella e formando neutroni, rendendone così i nuclei sempre più ricchi a spese dei protoni originari; la conseguenza è che il rapporto neutroni/protoni aumenta, creando nuclei che in condizioni normali sarebbero altamente instabili e decadrebbero quasi istantaneamente, ma che ora risultano stabili visto l’alto livello di Fermi degli elettroni e al gas degenere; contemporaneamente, grazie alla cattura elettronica, la pressione del gas cala e le forze gravitazionali possono continuare il loro lavoro di compressione.
Scendendo verso le profondità della stella, al crescere della densità i nuclei tenderanno ad avere un numero di massa sempre maggiore: fino a un ρ<1011 g/cm3 (ρ è rho, o ro: la diciassettesima lettera dell’alfabeto greco, e indica la densità) prevarranno quelli con numero di massa attorno agli 80, mentre arrivati a ρ=2×1011 g/cm3 predomineranno quelli vicini a 120.
Arrivati ad una densità critica di 4,3×1011 g/cm3, inizia quello che viene chiamato il ‘gocciolamento di neutroni’, ovvero un fenomeno in cui questi ultimi iniziano a fuoriuscire dai nuclei, dato che la forza di coesione nucleare n-n è inferiore a quella p-p e non è più sufficiente a mantenerli coesi; questo processo continua scendendo sempre più in profondità fino alla dissoluzione totale dei nuclei, o, meglio, fino al punto in cui questi tendono ad avere una distribuzione della densità nello spazio sempre meno localizzata nei loro centri, arrivando a sovrapporsi attorno a un ρ=2×1014 g/cm3; il risultato è così un gas degenere di neutroni liberi, con la presenza di un 2 o 3% di elettroni e protoni a un ρ=3×1014 g/cm3.
A pressioni più elevate, andando verso il centro, neppure i neutroni riusciranno a sopravvivere, come vedremo.

Telescope tra il 1999 e il 2000 della Nebulosa del Granchio, al
cui centro troviamo una stella di neutroni. Crediti:NASA/JWST
Struttura di una Stella di Neutroni
Una volta terminata l’implosione della stella, otterremo un oggetto di una ventina di chilometri di diametro e fatto a strati, un po’ come una cipolla:
Atmosfera
All’esterno troviamo una sottile atmosfera di carbonio spessa solo 10 centimetri, con una temperatura di circa 2 milioni di gradi Kelvin e una densità simile a quella del diamante vista l’enorme gravità presente sulla superficie, ovvero circa 100 miliardi di volte a quella a cui siamo normalmente abituati (analisi ottenuta dalle recenti osservazioni da parte di Chandra sulla Pulsar presente in Cassiopea A).
Per confronto, la nostra atmosfera si innalza per circa 100 km e ha una densità al livello del mare di 0,001 g/cm3.
Crosta Esterna
Subito sotto troviamo la crosta esterna, profonda circa 200 metri con un ρ che va da ≃ 1×109 g/cm3 a ≃ 4×1011, costituita da nuclei che partono dal 56Fe negli strati superiori ma che aumentano di massa e soprattutto di neutroni a mano a mano che si scende, fino a quando non inizia il fenomeno del gocciolamento dei neutroni; si presume che il fenomeno grazie al quale un nucleo di 56Fe possa aumentare di massa fino a divenire ad esempio 122Rb, fenomeno tutt’altro che banale, sia dovuto alla fotodisintegrazione di alcuni nuclei in particelle α e alla ricombinazione di queste ultime.
Grazie all’estrema gravità, le eventuali ‘montagne’ presenti sulla superficie sarebbero alte non più di qualche frazione di millimetro
Crosta Interna
C’è poi la crosta interna, spessa circa un chilometro e che arriva ad un ρ ≃ 2×1014g/cm3, pari alla densità nucleare, e che è composta da un reticolo cristallino di nuclei, elettroni relativistici e un superfluido di neutroni.
Questa zona finisce quando i nuclei iniziano a dissolversi
Nucleo Esterno
Il nucleo esterno invece è essenzialmente costituito da neutroni superfluidi, con una piccola percentuale di protoni superconduttivi ed un’identica quantità di elettroni degeneri relativistici, necessari per mantenere un equilibrio nelle cariche elettriche e che poi scompaiono completamente nella parte più interna (si arriva fino a un ρ circa doppio alla normale densità nucleare).
A queste densità inizia la creazione di particelle che normalmente non sono stabili in condizioni normali: attorno a un ρ di 2×1014g/cm3, il livello di Fermi degli elettroni raggiunge quello della massa di un muone (particella che come simbolo μ, che a riposo ha una massa di 105 MeV), e a questo punto diviene più conveniente introdurre un muone negativo con energia cinetica nulla piuttosto che creare un elettrone con un’alta energia cinetica.
 Nucleo Interno
Nucleo Interno
Il nucleo interno è ancora più interessante: viste le estreme densità ed energie raggiunte, vengono a crearsi le condizioni per cui è più conveniente creare degli iperoni ‘pesanti’ piuttosto che mantenere dei semplici neutroni, che hanno una massa a riposo minore; iniziano così ad essere create particelle come Σ⁻, Λ⁰ e altre ancora, con masse sempre più elevate a mano a mano che la pressione aumenta.
Altre teorie poi prevedono l’esistenza al centro di questi corpi celesti di un plasma di quark in stato superconduttivo e di gluoni, e altre ancora che ipotizzano la formazione in tali condizioni di quella che viene chiamata ‘materia strana’, formata da quark strani e che si presume possa addirittura rimanere stabile al di fuori di quelle immense pressioni; capire quali di queste teorie corrisponda al vero è tutt’ora una questione molto delicata e ben lungi dall’essere completamente chiarita, anche perché non è neppure sicuro che si riescano a raggiungere tali densità senza che la stella collassi definitivamente in un buco nero.
Tuttavia osservazioni recenti effettuate con l’osservatorio a raggi X Chandra hanno trovato due candidate precedentemente considerate stelle di neutroni ‘normali’, dove una risulta molto più piccola e l’altra molto più fredda di quello che dovrebbero essere secondo le leggi fisiche oggi conosciute, suggerendo l’ipotesi che esse siano composte da materia più densa del neutronio; queste deduzioni sono comunque messe in dubbio da parecchi ricercatori, e non sono conclusive.
Stelle da record
Con queste premesse, arrivare a stracciare dei record è molto facile, vediamoli insieme:
Campo Magnetico
Alcune stelle di neutroni hanno dei campi magnetici miliardi di volte di quello terrestre (che è di circa 50 μTesla), e in questi casi prendono il nome di Magnetar (contrazione di ‘Magnetic Star’).
Attualmente se ne conoscono meno di 30, e quella che ha la palma per il campo magnetico più potente sembra essere la SGR 1806−20, una stella sita a 42.000 anni luce da noi il cui campo, secondo il McGill Online Magnetar Catalog, arriva alla bellezza di 2×1011 Tesla.
Tenete presente che una simile intensità ucciderebbe qualunque essere umano lacerandone i tessuti a una distanza di oltre 1000 km per via del diamagnetismo dell’acqua, e che arriverebbe a smagnetizzare una carta di credito a una distanza corrispondente a quella dalla Terra alla Luna; inoltre questi campi deformano le strutture orbitali degli atomi facendo loro assumere la forma di un sigaro, così che, sottoponendo un atomo di idrogeno a un campo di 1010 Tesla, questo si allunga di 200 volte il proprio diametro originario.
Velocità di Rotazione
Tutti sappiamo che il periodo di rotazione terrestre è di 24 ore (un giorno), mentre il Sole ruota attorno al proprio asse in 27 giorni circa; quando però una stella collassa su se stessa, a causa della legge di conservazione del momento angolare (così come una pattinatrice che accelera la sua rotazione chiudendo le braccia), la stella è costretta ad accelerare in maniera vertiginosa la propria rotazione.
Tipicamente, le stelle di neutroni ruotano su se stesse con periodi che vanno da 1 a 30 secondi, ma uno studio del 2007 ha rilevato che la pulsar chiamata XTE J1739-285 ha un periodo di poco superiore ai 0,8 millisecondi (anche se in tempi successivi altri astronomi non sono riusciti ad ottenere lo stesso risultato), quindi la palma andrebbe a PSR J1748-2446ad, con una velocità di rotazione di 716 giri al secondo.
C’è comunque un limite alla velocità di rotazione raggiungibile: se questa superasse infatti i 1.500 giri al secondo, nonostante l’intensissima attrazione gravitazionale le pulsar potrebbero andare in pezzi; inoltre, oltre i 1.000 giri al secondo le stelle perderebbero più velocemente energia di quanto il processo di accrescimento possa renderle veloci grazie alla produzione di onde gravitazionali.
Gravità
Le stelle di neutroni sono gli oggetti ‘solidi’ (quindi buchi neri esclusi) con il campo gravitazionale più intenso sulla loro superficie, che arriva ad essere cento miliardi di volte (1011) quello terrestre, e quindi una monetina da un euro peserebbe lì come 200.000 (duecentomila) elefanti sulla Terra; questo comporta anche una velocità di fuga elevatissima, che è circa un terzo della velocità della luce nel vuoto (100.000 km/s).
Sono valori enormi: se un malcapitato astronauta volesse avventurarsi sulla sua superficie, nell’improbabile caso che riuscisse ad atterrare sano e salvo (dovrebbe sopportare enormi forze mareali mentre si avvicina, proprio come succede avvicinandosi ad un buco nero), verrebbe stritolato, schiacciato e infine annichilito dal calore presente e da quello generato dai suoi atomi leggeri, che subirebbero una fusione nucleare.
Densità
Beh, che dire, ci piace vincere facile 🙂
La densità nel nucleo interno, secondo quanto teorizzato, sarebbe dell’ordine dei 1015gr/cm3, ovvero l’equivalente di oltre 2.000.000.000 (due miliardi!) di elefanti per ogni cucchiaino da tè di detta sostanza (10 ml), oppure 1.400 (millequattrocento!) piramidi di Cheope, se preferite!
Da tenere presente che la densità all’interno di un nucleo atomico in condizioni normali è dell’ordine dei 1014g/cm3
Pressione
Qua è più difficile fare mente locale, visto che non abbiamo nessuna pietra di paragone a noi familiare che si possa facilmente usare.
Come stima dell’ordine di grandezza, diverse fonti riportano una pressione all’interno del nucleo di una stella di neutroni un valore di circa 1035 Pa (Pascal); ora, tenuto conto che 105 Pa equivalgono circa alla pressione dell’aria sulla superficie terrestre, avremo che la pressione al centro di una stella di neutroni è in una prima approssimazione equivalente a:
- 1030 volte la pressione dell’aria al livello del mare (P = 105 Pa)
- 1027 volte la pressione nella Fossa delle Marianne (P = 108 Pa)
- 2,5×1023 volte la pressione al centro della Terra (P = 4×1011 Pa)
- 3×1018 volte la pressione esistente nel centro del Sole (P = 3×1016 Pa)
Numeri a cui è difficile dare un senso; diciamo quindi solo che, nel centro di una stella di neutroni, la pressione è circa tre miliardi di miliardi di volte più forte che nel centro del Sole.
E ho detto tutto.
Riferimenti
- Bernardini, C. Guaraldo: Fisica del Nucleo
- Gittins, N. Andersson: Modelling neutron star mountains in relativity
Craig Heinke:Chandra X-Ray Observatory -Chandra Peers into Neutron Stars
Andrew W. Steiner: neutronstars.utk.edu
NASA’s HEASARC: Education& Public Information (per dimensioni e spessori degli strati)
Chandra X-Ray Observatory: press_110409
L’articolo è pubblicato in COELUM 266 VERSIONE CARTACEA



















