La teoria di Ramsey
Se fin dai tempi più remoti l’uomo ha creduto di scorgere nel cielo forme familiari, profili di personaggi mitologici, sagome di animali esistenti sulla Terra o fantastici, lo dobbiamo forse a una teoria matematica sviluppata nel 1928 da un venticinquenne inglese: Frank Plumpton Ramsey.
Nell’articolo di gennaio ho accennato alla vicenda di questo genio della matematica, che fu anche un brillante logico e un illustre economista. Ramsey nacque e crebbe a Cambridge, dove suo padre, insegnante di matematica, era preside del prestigioso Magdalene College.
Dopo il diploma, conseguito nel 1925, Ramsey si unì al gruppo di ricerca coordinato dal celebre economista John Maynard Keynes, e scrisse un paio di articoli di economia matematica tuttora molto citati.
Nel giro di pochi anni si occupò anche di logica, di filosofia, di statistica e teoria della probabilità, di psicologia cognitivista e semantica. Chi lo conosceva lo descriveva come un pensatore cristallino, sempre in grado di costruire ragionamenti perfettamente coerenti e di evitare trappole logiche.
Nel 1930 dovette sottoporsi a una operazione chirurgica addominale, e purtroppo, per le complicazioni sopraggiunte dopo l’intervento, morì tragicamente prima del suo ventisettesimo compleanno.
La teoria che Ramsey sviluppò nel 1928 afferma che in qualsiasi struttura abbastanza ricca di elementi, non importa se si tratta di un insieme di stelle, o di un gruppo di persone, o di una sequenza di numeri, è inevitabile osservare delle configurazioni regolari. In altre parole, anche dove il caos sembra regnare, esiste sempre un po’ di ordine.
Ma quanto ricca deve essere la struttura considerata, per far emergere l’ordine dentro di sé? Questa è la difficile domanda connessa alla teoria di Ramsey. La risposta dipende ovviamente dal tipo di problema ramseyano che viene studiato.
Nell’articolo di gennaio descrivevo il famoso esempio della festa: quanti devono essere gli invitati a un ricevimento per essere certi che tre di loro si conoscano l’un l’altro oppure che tre di loro non si conoscano a vicenda?
Per risolvere il rompicapo, si potrebbe pensare di considerare tutte le possibili combinazioni e verificare se in ognuna c’è un terzetto di reciproci conoscenti o un terzetto di totali estranei. Ma quante sono le possibili combinazioni? Per una festa con 6 invitati, vi sono 15 relazioni interpersonali da prendere in esame: infatti per ognuna delle 6 persone ci sono 5 altre persone con cui avere a che fare, ma per evitare di considerare ogni legame due volte, dobbiamo dividere per 2: quindi (6 × 5) / 2 = 15). Dato che ognuna di queste 15 relazioni può essere di conoscenza o di estraneità, le possibili combinazioni sono 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2, ovvero, scritto in modo più compatto come amano fare i matematici, 215, che è uguale a 32.768.
Non appena si considerano feste più affollate, questo algoritmo di “forza bruta” diventa decisamente poco efficiente. In realtà esiste un approccio molto più semplice per risolvere il problem. Immaginiamo che i 6 invitati si chiamino Antonella, Bruno, Cinzia, Davide, Elena e Fausto. Supponiamo che Antonella conosca almeno tre delle altre persone: ad esempio Bruno, Cinzia e Davide. Ora, se Bruno e Cinzia, oppure Bruno e Davide, oppure Cinzia e Davide si conoscono tra di loro, allora Antonella e la coppia di conoscenti sono un terzetto di reciproci conoscenti; altrimenti Bruno, Cinzia e Davide sono un terzetto di totali estranei.
Supponiamo invece che Antonella conosca non più di due fra le altre persone: ad esempio Bruno e Cinzia. Se Davide ed Elena, oppure Davide e Fausto, o Elena e Fausto non si conoscono tra di loro, ecco che Antonella e la coppia di estranei sono tre persone che non si conoscono tra loro; altrimenti Davide, Elena e Fausto sono un trio di conoscenti. Abbiamo facilmente dimostrato che in un gruppo di sei persone devono esserci per forza tre conoscenti o tre estranei!
Se la festa avesse soli 5 invitati, invece, questa certezza non esisterebbe: in questo caso, infatti, potreste facilmente trovare una “configurazione” di conoscenze in cui non esiste alcun terzetto di reciproci conoscenti o di totali estranei.
Diversi problemi di Ramsey ammettono soluzioni diverse. Tuttavia vale sempre il concetto fondamentale: esiste una soglia di complessità del sistema considerato sopra la quale esistono sicuramente strutture ordinate di un certo tipo.
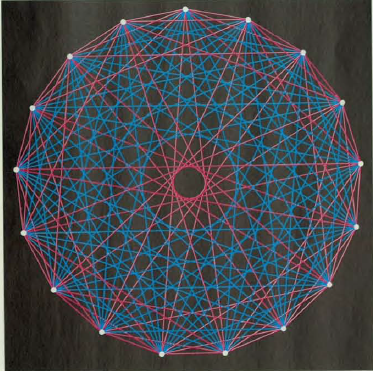
Se, anziché ricercare terzetti di conoscenti o di estranei, fossimo interessati ai quartetti, avremmo bisogno di 18 invitati. La figura seguente mostra un esempio di festa con 17 persone, in cui non esistono quartetti di reciproci conoscenti o di totali estranei: gli invitati sono rappresentati dai pallini bianchi, le relazioni di conoscenza e di estraneità rispettivamente dalle linee rosse e dalle linee blu.
Il problema analogo relativo a quintetti e sestetti, invece, è tuttora irrisolto.
Negli anni Sessanta del secolo scorso, due ricercatori americani, Alfred Hales e Robert Jewett, provarono ad applicare la teoria di Ramsey al gioco del tris, e dimostrarono che versioni abbastanza “ricche” del gioco portano sempre alla vittoria di uno dei due giocatori, rendendo impossibili le “patte”.
Che cosa s’intende per versioni ricche? Il tris classico si gioca su una scacchiera bidimensionale 3 × 3, ma nessuno ci vieta di immaginare versioni tridimensionali, o in generale a N dimensioni (con N ≥ 2), e possiamo anche pensare a scacchiere di dimensioni via via crescenti.
Per esempio, Hales e Jewett trovarono che, in un tris giocato su un cubo tridimensionale 3 × 3 × 3, comunque vengano collocati i cerchietti e le croci, la partita finirà sicuramente con tre cerchi in fila o con tre croci in fila.
L’enigma
I lettori di Coelum che si sono cimentati nella risoluzione dell‘enigma di gennaio hanno dovuto rompersi un po’ la testa sulle “triplette” nascoste all’interno di successioni di numeri interi. Una tripletta contenuta in una successione è una sequenza di tre numeri della successione posti in progressione aritmetica. Per esempio, nella successione 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, sono triplette valide (1, 5, 9), oppure (2, 3, 4), oppure (4, 6, 8), e così via.
Il quesito era il seguente.
Prendiamo i numeri interi compresi tra 1 ed N, e coloriamo ciascuno di essi di rosso o di blu, a nostro piacere. Quanto deve essere grande N perché, comunque scegliamo la colorazione dei numeri, vi siano sicuramente delle triplette dello stesso colore?
Nell’articolo, facevo notare che N = 7 è un valore ancora troppo basso: un controesempio è dato dalla successione 1 2 3 4 5 6 7, in cui non esistono triplette monocromatiche. È sufficiente prendere N = 8 per far comparire inevitabilmente le triplette monocolore? Oppure occorre salire a N = 9? Oppure ancora più in alto? O forse, per quanto si aumenti il valore di N, si può sempre evitare l’insorgenza di triplette dello stesso colore? (quest’ultima possibilità, come potete notare, sarebbe contraria alla teoria di Ramsey…)
Il problema delle triplette monocromatiche fu sollevato nel 1926 da un matematico olandese, Bartel Leendert van der Waerden, il quale si accorse che, non appena N diventava abbastanza grande, le triplette monocromatiche saltavano fuori sempre. Lo studioso trovò che il fenomeno si applicava anche al caso di sequenze più grandi delle triplette: in generale gruppi di M numeri separati tra di loro per progressione aritmetica.
Per dimostrare rigorosamente il teorema, van der Waerden chiese l’aiuto dei colleghi Emil Artin e Otto Schreier. Lo stesso van der Waerden, qualche anno dopo, scrisse:
Andammo nell’ufficio di Artin, al Dipartimento di matematica dell’Università di Amburgo, e cercammo di trovare una dimostrazione. Tracciammo qualche diagramma sulla lavagna. Avevamo quelle che in tedesco si chiamano Einfiille: idee improvvise che vengono fulminee alla mente. Più volte queste nuove idee impressero una svolta alla discussione e alla fine una di esse portò alla soluzione.
Alla fine van der Waerden escogitò una tecnica di dimostrazione basata su una forma particolare di induzione. Il risultato è, evidentemente, un’ulteriore applicazione della teoria di Ramsey, e non a caso viene spesso ricordato come teorema di Ramsey per le progressioni aritmetiche. In molti casi viene però menzionato come teorema di van der Waerden.
Secondo il teorema di van der Waerden, quindi, l’enigma di gennaio ha senso. Ma rimane il problema: quanto deve essere lunga la successione di interi affinché, colorandola arbitrariamente, le triplette monocolore compaiano con certezza?
La soluzione e i vincitori
La risposta al quesito posto era N = 9. Attraverso quale ragionamento si poteva arrivare alla risposta corretta? Evidentemente occorreva trovare un valore di N -1 per il quale esisteva una colorazione che non generava triplette monocromatiche, e mostrare che, invece, già per N, diventava inevitabile la comparsa di tali famigerate strutture.
Ebbene, coloriamo come segue la successione dei primi N – 1 = 8 interi:
1 2 3 4 5 6 7 8
Come potete vedere, non ci sono triplette né rosse né blu.
Con N = 9, invece, indipendentemente dallo schema di colorazione adottato, ci possiamo trovare in due casi:
- • il 4 e il 6 hanno lo stesso colore
oppure
- • il 4 e il 6 sono di colore diverso.
Analizziamo il primo caso, e supponiamo che il 4 e il 6 siano colorati di blu:
1 2 3 4 5 6 7 8 9
Per evitare la tripletta (4, 5, 6), il 5 deve essere colorato di rosso:
1 2 3 4 5 6 7 8 9
Ora, per evitare le triplette (2, 4, 6) e (4, 6, 8), dobbiamo colorare di rosso anche il 2 e l’8:
1 2 3 4 5 6 7 8 9
Notate qualcosa di strano? Eh già, è comparsa la tripletta (2, 5, 8). Cercando di evitare le triplette blu, si è creata una tripletta rossa!
Consideriamo ora il secondo caso, in cui il 4 e il 6 sono di colore diverso: per esempio il 4 è rosso e il 6 è blu:
1 2 3 4 5 6 7 8 9
Possiamo allora colorare il 5 di rosso o di blu senza che si crei una tripletta. Decidiamo di colorarlo di rosso:
1 2 3 4 5 6 7 8 9
A questo punto, siamo costretti a colorare di seguito:
- • il 3 di blu, per evitare la tripletta (3, 4, 5)
- • il 9 di rosso, per evitare la tripletta (3, 6, 9)
- • il 7 di blu, per evitare la tripletta (5, 7, 9)
- • l’8 di rosso, per evitare la tripletta (6, 7, 8)
- • il 2 di blu, per evitare la tripletta (2, 5, 8)
- • l’1 di rosso, per evitare la tripletta (1, 2, 3)
La successione finale è quindi la seguente:
1 2 3 4 5 6 7 8 9
Ma attenzione! C’è anche qui una tripletta monocromatica: (1, 5, 9)!
Abbiamo quindi dimostrato che, comunque si colori la successione iniziale, le triplette ci sono per forza.
A inviarci per primo la risposta corretta e una dimostrazione valida è stato DARIO BROGGI, che quindi ha vinto l’abbonamento premio. Hanno inviato soluzioni corrette anche Daniele Tosalli e Maurizio Carlino. Quest’ultimo, com’è sua abitudine, ha spedito una rigorosa e magnifica analisi del problema. I nostri più vivi complimenti a tutti loro!
