Il Paradosso
Prende il nome dall’astronomo tedesco Heinrich Wilhelm Olbers, che lo propose nel 1826. In realtà era già stato descritto da Keplero nel 1610 e dagli astronomi Halley e Cheseaux nel XVIII secolo. I presupposti di base perché il paradosso sia tale sono:
1. che l’Universo abbia estensione infinita
2. che l’Universo esista da infinito tempo e sia immutabile
3. che l’ Universo sia omogeneo ed isotropo, ovvero le stelle siano disposte in modo uniforme nello spazio
Il Paradosso di Olbers ha il seguente enunciato: come è possibile che il cielo notturno sia buio nonostante l’infinità di stelle presenti nell’Universo?
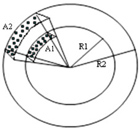
Per comprendere meglio la problematica si supponga che le stelle siano distribuite uniformemente in “strati”, concentrici, con la stessa densità ovunque. Si prendano due sfere di raggio R1 e R2.
Nella superficie A1 ci saranno N1 stelle, mentre in A2 ce ne saranno N2, inoltre N1/ N2 = A1/A2 cioè il numero di stelle entro un settore sferico è, proporzionale all’area del settore stesso.
La superficie di una sfera di raggio R è proporzionale a R2, quindi
N1/ N2 = R12/R22
Si supponga che ogni stella abbia la stessa luminosità L.
La sua luminosità apparente è proporzionale a 1/R2, dove R è la sua distanza. In definitiva, la luminosità totale apparente di tutte le stelle che si trovano lungo la sfera di raggio R1 è
L1 = N1L/4pR12
mentre la luminosità totale apparente delle stelle che si trovano lungo la sfera di raggio R2 è
L2 = N2L/4pR22
dunque
L1/L2 = (N1/R12)/(N2/R22) ma
N1/N2 = R12/R22
quindi L1 = L2, cioè da ognuna di queste sfere ci arriva la stessa quantità di luce.
Ogni sfera produce una luminosità uguale alla precedente che si somma a quella delle altre. Considerando che l’ Universo è infinito e omogeneo, esistono infinite sfere di spazio di raggio sempre più grande. Pertanto la quantità di luce che arriverebbe a noi da queste infinite sfere concentriche dovrebbe essere tale che anche di notte dovremmo avere la stessa luminosità che di giorno (paradosso di Olbers). Al fine di una migliore comprensione di quanto seguirà è utile osservare che abbiamo supposto le stelle distribuite in “strati” concentrici di cui abbiamo considerato le relative superfici.
Questa è una semplificazione concettuale che contribuisce a rendere il paradosso di Olbers difficile da spiegare. In realtà le stelle non si trovano distribuite su una superficie ma in un volume. Inoltre le variazioni di volume di una sfera, all’aumentare del raggio della stessa, hanno trend differenti rispetto alle variazioni della sua superficie.
