Abbonato a vita – approfondimenti sul quesito e soluzione

Il problema di Roberto

Ricordate il numero 183 di Coelum, l’ultimo dell’epoca dell’edicola? Nell’ultima pagina raccontavo la storia di Roberto, giovane appassionato di astronomia e avido lettore della prestigiosa rivista che state sfogliando.

A partire dal mese di settembre 2014, il quattordicenne Roberto è abbonato a Coelum. Ogni primo giorno del mese riceve comodamente a casa la sua rivista preferita, e gli occorrono sempre esattamente trenta giorni per leggere a fondo ogni numero.

Come osservavo nell’articolo, chi è folgorato in giovane età dalle meraviglie del cielo è molto probabile che rimanga un astrofilo per tutta la vita. Possiamo immaginare che sarà così anche per Roberto: non stupisce allora sorprenderlo, in un nostro immaginario viaggio nel futuro, mentre festeggia il suo centenario con il numero di Coelum di settembre 2100 illuminato dalle candeline della torta.

La sfida lanciata ai lettori era la seguente:

Quanti sono esattamente, dal primo settembre 2014 al primo settembre 2100, i giorni nei quali Roberto si ritroverà a sfogliare le ultime pagine del numero del mese precedente, avendo già sul comodino il numero nuovo?

Molti lettori si sono cimentati con il problema, ma soltanto due hanno risposto esattamente. Vediamo perché.

Analisi del problema

A ben vedere, dal punto di vista di Roberto, ci sono tre “tipi” di giorni in un anno:

• • i giorni “normali”, che chiamerò di “tipo A”, nei quali il ragazzo legge il numero che gli è arrivato il primo giorno del mese in corso;
• • i giorni “di tipo B”, in cui Roberto ha già terminato la lettura dell’ultimo numero ricevuto, ma non può iniziare a leggere il successivo perché non gli è ancora arrivato;
• • i giorni “di tipo C”, in cui il giovane astrofilo ha già ricevuto il numero del mese in corso, ma sta ancora terminando la lettura del numero del mese precedente.

Per esempio, consideriamo il mese di gennaio 2015. Il postino recapiterà il numero 188 il primo del mese (non formalizziamoci sul fatto che è alquanto improbabile che la posta arrivi il giorno di Capodanno, così come in altri giorni festivi coincidenti con il primo del mese).

Roberto impiegherà i primi 30 giorni di gennaio per leggere il numero: questi saranno giorni di tipo A. Il 31 gennaio è un giorno di tipo B, perché il numero 189 non è ancora giunto a casa di Roberto. Il mese di febbraio 2015 ha 28 giorni, cosicché Roberto lo trascorrerà tutto leggendo il nuovo numero, ma gli serviranno anche i primi due giorni di marzo per completare la lettura: questi saranno quindi due giorni di tipo C.

E così via. Se completiamo l’analisi dell’anno, ci accorgiamo che il 2015 contiene 35 giorni di tipo B (il 31 gennaio, il 31 luglio, tutti i 31 giorni di agosto, il 31 ottobre, il 31 dicembre), e 4 giorni di tipo C (i primi due giorni di marzo, il primo aprile). Tutti gli altri 356 giorni sono di tipo A.

La figura seguente illustra la distribuzione dei tre tipi nel corso dell’anno (in verde i giorni di tipo A, in viola quelli di tipo B, in rosso quelli di tipo C).

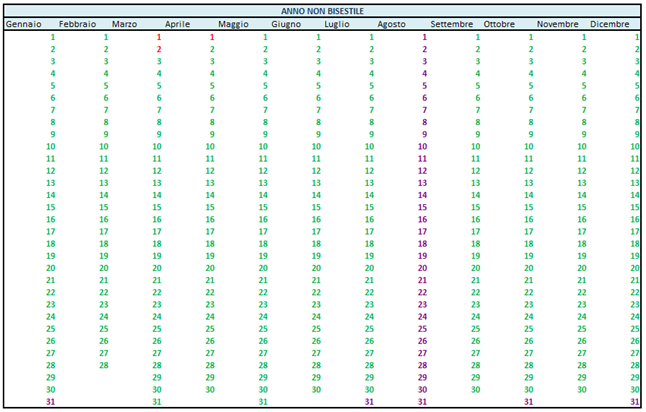
I miei lettori avranno sicuramente colto la questione fondamentale: questa ripartizione vale non solo per il 2015, ma per tutti gli anni non bisestili.

In un anno bisestile, invece, le cose cambiano: i primi 30 giorni di gennaio rimangono di tipo A, e il 31 gennaio è ancora di tipo B. Il mese successivo, però, ha in questo caso 29 giorni, il che significa che a Roberto basta il primo marzo per terminare la lettura del numero di febbraio. E questo provoca conseguenze sulla suddivisione dei giorni del resto dell’anno.

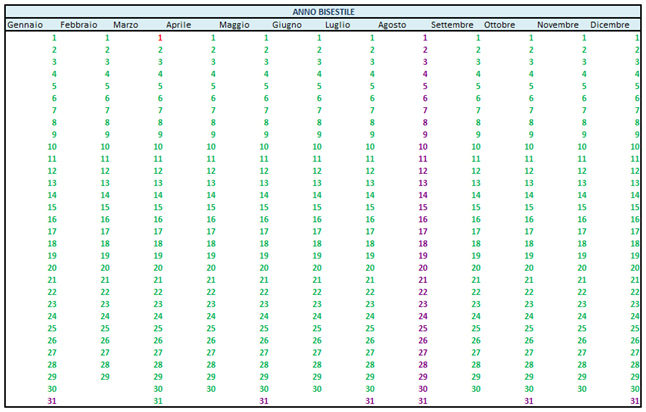
In generale, un anno bisestile contiene 36 giorni di tipo B (oltre a quelli tipici degli anni non bisestile, dobbiamo considerare infatti il 31 maggio), e un solo giorno di tipo C (il primo marzo). E tutti gli altri 358 giorni sono di tipo A. La figura seguente mostra tale ripartizione.

Calendari e anni bisestili

Appare ora chiaro dove si trova la chiave della risoluzione del problema: basta contare quanti anni bisestili ci sono tra il 2015 e il 2100 e il gioco è fatto.

Ebbene, nel periodo considerato ci sono 86 anni, di cui 21 bisestili (2016, 2020, 2024, 2028, 2032, 2036, 2040, 2044, 2048, 2052, 2056, 2060, 2064, 2068, 2072, 2076, 2080, 2084, 2088, 2092, 2096) e 65 non bisestili (tutti gli altri).

E il 2100? Perché non l’ho incluso tra i bisestili? In fin dei conti gli anni divisibili per 4 sono tutti bisestili, o no?

No. Se un anno divisibile per 4 lo è anche per 100, non è bisestile. E non è finita qui. Questa eccezione contiene, infatti, a sua volta, un’eccezione: Se l’anno è divisibile per 400, è comunque bisestile. L’esempio più emblematico è molto recente: il Duemila, anno divisibile per 4 ma secolare, è stato bisestile perché divisibile per 400.

Questo meccanismo, che potrebbe apparire cervellotico, è in realtà il geniale risultato dell’introduzione del calendario gregoriano, nel 1582.

Papa Gregorio XIII promulgò in quell’anno la bolla Inter gravissimas, che riformava il vecchio calendario giuliano, in vigore fin dai tempi di Giulio Cesare.

Come nel calendario giuliano, anche l’anno gregoriano non bisestile comprende 365 giorni, e quello bisestile introduce un giorno aggiuntivo al mese di febbraio.

La durata in giorni dei diversi mesi è per tutti molto familiare: gennaio, marzo, luglio, agosto, ottobre e dicembre hanno 31 giorni; aprile, giugno, settembre e novembre ne hanno 30, mentre febbraio ha 28 giorni negli anni ordinari e 29 in quelli bisestili.

Vi sono molte tecniche mnemoniche per ricordare la lunghezza dei vari mesi: dalle regole: dall’osservazione delle nocche delle mani e degli infossamenti fra di loro, alle popolari filastrocche come la seguente:

Trenta giorni ha novembre

con april, giugno e settembre

di ventotto ce n’è uno

tutti gli altri ne han trentuno.

Ma a noi interessa soprattutto la distribuzione degli anni bisestili. Dato che nel calendario giuliano, cioè prima del 1582, gli anni bisestili si alternavano semplicemente ogni 4 anni, la durata media dell’anno giuliano medio era pari a (365+365+365+366)/4, cioè 365,25 giorni.

Questa durata, però, era maggiore di quella dell’anno solare medio, ben nota agli astronomi (e anche agli astrofili), che equivale a circa 365,2422 giorni: più di 11 minuti di differenza all’anno.

Di conseguenza, nel corso dei secoli, l’utilizzo del calendario giuliano provocò l’accumularsi di un ritardo rispetto alle stagioni reali, pari a circa un giorno ogni 128 anni.

Verso la fine del sedicesimo secolo, lo sfasamento era ormai di circa 10 giorni. Secondo le osservazioni degli astronomi, la primavera non cominciava più il 21 marzo, ma l’11 marzo. La Pasqua, che cade la prima domenica successiva al plenilunio di primavera, veniva festeggiata quindi in una data “sbagliata”.

Quando gli astronomi gli fecero notare il problema, papa Gregorio XIII comprese che di questo passo si sarebbe finiti per celebrare la Pasqua in estate. Il pontefice si decise allora ad affrontare la questione, e nel 1580 nominò una commissione di esperti con il compito di trovare una soluzione allo spinoso dilemma.

Nella commissione figuravano alcuni autorevoli matematici e astronomi dell’epoca, alcuni dei quali italiani: Luigi Lilio, calabrese, probabilmente il vero ispiratore della soluzione che alla fine venne adottata; Cristoforo Clavio, gesuita tedesco e professore nel Collegio Romano; Giuseppe Scala, siciliano, giovane professore all’università di Padova; Vincenzo di Lauro, anche lui calabrese, vescovo di Mondovì e consigliere teologico; Pedro Chacòn, spagnolo, teologo ed esperto in patristica e di storia della chiesa; Ignazio Nehemet, patriarca di Antiochia di Siria, anche lui storico della chiesa; Ignazio Danti, frate domenicano di Perugia e vescovo di Alatri.

Per fissare la durata dell’anno solare medio, gli scienziati presero come riferimento le misurazioni di Niccolò Copernico, pubblicate pochi anni prima, nel 1543.

Il 14 settembre 1580 la commissione consegnò nelle mani del papa il loro resoconto finale, intitolato Ratio corrigendi fastos confirmata et nomine omnium, qui ad Calendarii correctionem delecti sunt, oblata Sanctissimo Domino nostro Gregorio XIII.

Dalla relazione emergeva che due cose erano necessarie per risolvere il problema del calendario:

• 1. riallineare la data d’inizio delle stagioni con quella vigente nell’anno 325;
• 2. modificare la durata media dell’anno, in modo da prevenire il ripetersi di questo problema.

Per attuare il primo punto, si stabilì che il giorno successivo al 4 ottobre 1582 sarebbe stato il 15 ottobre 1582. Per il secondo punto, invece, si introdussero l’eccezione e la “sub-eccezione” menzionate prima: gli anni divisibili per 100 non sono bisestili, a meno che non siano divisibili anche per 400.

Il calendario gregoriano entrò in vigore già il 15 ottobre 1582 in Italia, Francia, Spagna, Portogallo, Polonia–Lituania e Belgio–Olanda–Lussemburgo, mentre alcuni degli altri paesi cattolici (Austria, Boemia, Moravia e cantoni cattolici della Svizzera) si adeguarono con qualche anno di ritardo. L’adozione del calendario gregoriano negli altri stati fu invece molto più lenta.

Con l’introduzione della nuova regola degli anni bisestili, l’anno gregoriano medio diventò un po’ più corto di quello giuliano, e questa differenza è legata a quei 3 anni su 400 che cessavano di essere bisestili: l’equivalente di 10 minuti e 48 secondi in meno rispetto a prima.

Quanto bastò a riallineare quasi perfettamente le cose: la discrepanza rispetto alla realtà è infatti di soltanto un giorno ogni 3323 anni circa. Possiamo essere abbastanza soddisfatti.

La soluzione del problema di Roberto

Torniamo ora al problema di Roberto.

Appurato che nel periodo compreso tra il 2015 e il 2100 ci sono 86 anni, di cui 21 bisestili e 65 non bisestili (tra cui il 2100), il problema si riduce al contare quanti sono in tutto, nel periodo compreso tra il 2015 e il 2100, i giorni di tipo C.

Presto detto: abbiamo visto che in ognuno dei 21 anni bisestili esiste un solo giorno di tipo C, mentre in ognuno dei 65 anni non bisestili vi sono 4 giorni di tipo C. La formula da utilizzare è quindi la seguente:

Numero giorni di tipo C = 1 × 21 + 4 × 65 = 21 + 260 = 281

La risposta corretta al quesito di luglio-agosto è quindi 281.

I vincitori

I lettori che hanno risolto correttamente l’enigma di Roberto sono stati due: Daniele Tosalli e Michele D’Errico. Entrambi hanno giustificato esaurientemente la risposta.

Dato che Tosalli ha recentemente già vinto l’abbonamento, il vincitore del numero 183 è Michele D’Errico.

Altri lettori hanno proposto risposte diverse, quindi errate: qualcuno ha detto 278 giorni, qualcun altro ha proposto 275, e qualcun altro ancora ha azzardato 323.

Complimenti a tutti coloro i quali hanno accettato la sfida e hanno provato a risolvere il problema di Roberto!