Ambigui Messaggi Arrivati dallo Spazio

1 Novembre 2005

26 views

Dagli esempi forniti si vede facilmente che il simbolo è utilizzato quando i due fattori hanno diversa parità, mentre il simbolo si utilizza quando i due fattori hanno la medesima parità; in altri termini, data la somma dei termini a e b, quando questa è pari si utilizza , mentre quando la medesima somma è dispari si utilizza .

I citati numeri a e b sono quelli che usiamo noi: chiamando m e n quelli che invece appaiono nei calcoli “alieni”, non dovrebbe essere troppo difficile accorgersi che allora m-n=b e, nel caso del simbolo , vale anche m+n=a.

Gli esempi migliori dell’utilizzo dei simboli si vedono allora ricordando il prodotto notevole (a+b)(a-b)=a2-b2, perché si vede subito che:

e, rispetto al calcolo originale, le operazioni si traducono:

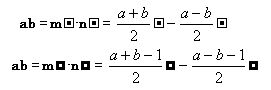Il metodo risulta forse più chiaro con una figura:

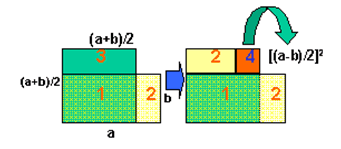
Si vedono un rettangolo di base a (orizzontale) e altezza b e un quadrato di lato (a+b)/2 avente base e lato sinistro sovrapposti agli omonimi elementi del rettangolo. L’area comune alle due figure (segnata con 1) è tratteggiata come pure sono tratteggiate la parte di rettangolo esterna al quadrato (2) e una zona equivalente a questa nella parte sinistra della parte del quadrato esterna al rettangolo (3); rimane così non tratteggiato un quadratino (4), di lato (a-b)/2, differenza tra l’area del quadrato e quella del rettangolo.
Come vi abbiamo detto nel problema, un nostro amico è riuscito a dedurre interessanti ipotesi sociologiche sugli abitanti del primo pianeta (chiamiamolo “Pianeta X”): vi riportiamo il testo integrale:
Trovata la chiave interpretativa del processo matematico che sta alla base della moltiplicazione della prima civiltà, è ovvio che ci si chieda in base a quale processo logico esso sia nato. Malgrado l’apparente assurdità di un tale procedimento, esso nasce invece certamente da un semplicissimo ragionamento, da considerarsi spontaneo se si tiene conto del fatto che la cultura aliena ha un’origine legata ad attività stanziali di tipo agropastorale; queste hanno portato ovviamente gli icsiani a privilegiare gli studi di geometria (di misurazione dei terreni!) rispetto a quelli algebrico numerici. La moltiplicazione basata sull’uso del nasce certamente dall’osservazione quasi banale che un rettangolo ha un’area un po’ più piccola di quella del quadrato cha ha per lato la semisomma (la media) dei lati del rettangolo; alla susseguente domanda, poi, “di quanto più piccola?”, risponde il disegno sopra, che mostra appunto che il “quanto più piccola” è l’area del quadrato cha ha per lato la semidifferenza dei lati del rettangolo.
L’uso del compare successivamente ed è legato all’introduzione dei numeri naturali ed alla primitiva esigenza di lavorare con numeri interi, per cui il metodo basato sui andava a meraviglia per il prodotto di numeri di uguale parità, ma cadeva in difetto per quello di numeri di diversa parità. Venne così introdotto il , definito come l’operatore che indica la somma del numero che lo precede col quadrato del numero stesso.
Per quanto riguarda invece il secondo messaggio, ormai addestrati dal primo si vede che:

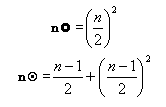e quindi, se i fattori hanno ugual parità:

ossia,

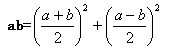mentre se i fattori hanno diversa parità:

ossia,

…e anche qui non poteva mancare un’analisi sociologica sugli abitanti del secondo pianeta (che chiameremo, naturalmente, “Pianeta Y”):
Il metodo di moltiplicazione utilizzato sul pianeta Y è di palese derivazione icsiana, sia dal punto di vista dei nomi e degli operatori utilizzati, che immediatamente ricordano e e, presumibilmente, vengono espressi in ipsiloniano con gli stessi suoni che in icsiano esprimono questi ultimi, sia dal punto di vista operativo metodologico, ma dimostra un assorbimento incompleto della cultura icsiana da parte degli ipsiloniani, per cui il metodo ipsiloniano sembra consistere in una faticosa ricostruzione mnemonica di quello icsiano, non capito a fondo. Ci troviamo così di fronte ad un metodo di moltiplicazione appesantito rispetto all’originale e che nasconde l’evidente bellezza e la semplicità logica del primigenio metodo “iano” degli icsiani. Sebbene i numeri sui quali agiscono gli operatori e siano legati in modo estremamente semplice ai due fattori del prodotto, essendone la somma e la differenza, l’azione di tali operatori ha una definizione che non risulta immediatamente illuminante; l’operatore dice infatti “dimezza il numero che mi precede e poi fanne il quadrato”, mentre l’operatore impone “togli uno dal numero che mi precede, dimezza il risultato e poi somma a quest’ultimo numero il suo quadrato”.
Esse riproducono dunque, in sostanza, le regole di moltiplicazione icsiane, ma queste ultime sono certamente, come abbiamo ampiamente mostrato, di interpretazione immediata, cosa che non ci sentiamo invece di affermare per quelle ipsiloniane.