L’astronautica è sempre alla ricerca del propellente perfetto: deve essere leggero, potente, occupare poco spazio, e liberare rapidamente energia; avete mai pensato che non esistono aerei diesel, proprio per queste ragioni? E se certe esigenze sono presenti già per la costruzione di aerei, pensate quali saranno le richieste per il perfetto combustibile per astronavi: a differenza di quelli destinati ad uso terrestre, il combustibile per lo spazio non deve aver bisogno d’ossigeno o d’aria – o, se proprio è necessaria, dovrà portarsela dietro. Dovrà essere drammaticamente poco pesante (anzi, pardon, massivo) ed eccezionalmente poco voluminoso, se non si vuole che i viaggi interplanetari si facciano su astronavi ridotte in pratica a serbatoi volanti. E’ certo per questo che i sistemi di trasporto immaginati dalla fantascienza non prendono mai in considerazione i combustibili fossili: antigravità, salti spaziali, vento solare… va bene tutto, basta che non si tiri in ballo nulla che assomigli neanche lontanamente alla benzina.
Nel nostro ultimo quiz, da diligenti matematici, abbiamo proposto forse proprio il combustibile perfetto, per il nostro viaggio fio ad Andromeda: le progressioni geometriche. Sono sempre affascinanti, e hanno una lunga tradizione anche nella narrativa, non solo nella matematica. Chi non ricorda la leggenda del giocatore di scacchi che, dopo aver battuto il potente re, chiese in premio solo un chicco di riso per la prima casella della scacchiera, due per la seconda, quattro per la terza, otto per la quarta, sedici per la quinta, e così via? Il povero re rimase davvero scioccato nello scoprire di non riuscire a soddisfare quella apparentemente misera richiesta (mai quanto fu scioccato l’astuto giocatore, che ci rimise la testa non appena si capì l’esosità della sua richiesta), ma in fondo non era altri che l’ennesima vittima delle progressioni geometriche. Progressioni che poi, a ben vedere, non sono neanche le più veloci della matematica: l’esponenziale, ad esempio, le batte tutte senza difficoltà; ma le geometriche hanno il pregio d’essere semplici, immediate, e le cose semplici sono sempre ricche di fascino.
A dimostrazione di questo fascino c’è anche il numero di soluzioni ricevute, che è senza dubbio il più alto della storia dei quiz di Rudi Mathematici per Coelum. Come sempre, citeremo solo una parte delle soluzioni ricevute, ma ci teniamo a specificare che questa volta la “parte” è proporzionalmente più piccola del solito.
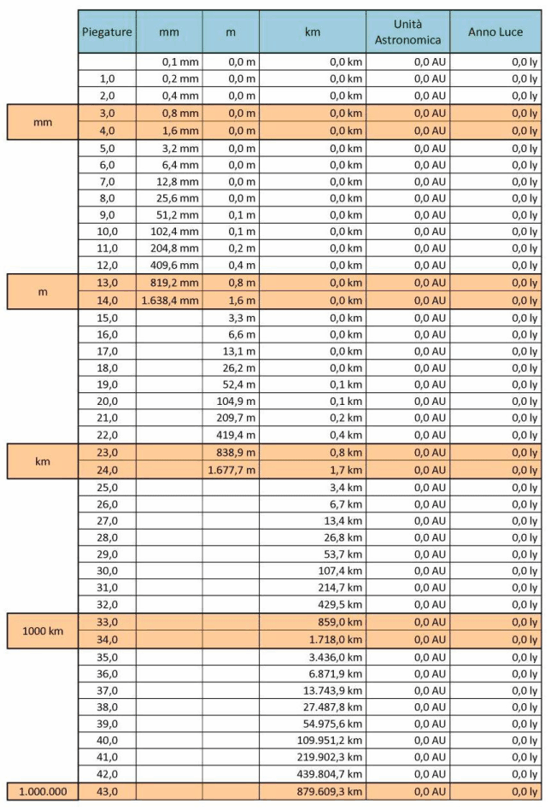
Orbene, il quiz, di per sé, era di esposizione abbastanza semplice: disponendo di un foglio di carta di spessore pari ad un decimo di millimetro, quante piegature serviranno per arrivare al centro della Galassia di Andromeda, supposta ad una distanza di 2,5 milioni di anni luce da noi? La risposta non è particolarmente complessa da trovare, ma bisogna avere un po’ di accortezza a non lasciarsi confondere dalle ripetute duplicazioni e a tenere sempre ben presenti le diverse unità di misura usate per la definizione dei dati iniziali del problema. Per toglierci subito il dente, potremmo affidarci alla chiara esposizione (e non meno chiara tabella) inviataci del nostro affezionato e già premiato Maurizio Leotta:
Questa Quante piegature occorrono per arrivare al centro della Galassia di Andromeda?
Distanza Galassia di Andromeda: 2.500.000 anni luce (ly)
Spessore foglio di carta: 0,1 millimetri (mm)
Costanti note:
1 Anno Luce (ly): 9.460.730.472.580.800 metri (m)
1 Unità Astronomica (AU): 149.597.870.691 metri (m)
Soluzione:
Ad ogni piegatura si raddoppia lo spessore seguendo la seguente progressione geometrica:
Termine ennesimo dato da: arn
Fattore di scala: a=0,1
Ragione: r=2
Numero piegature n.
Con n=87 si ottiene uno “spessore” del foglio piegato di 1.635.629,6 ly mentre con n=88 si ottiene un “spessore” di 3.271.259,1 ly. Quindi è tra questi due valori che si raggiunge la Galassia di Andromeda. Di seguito una tabella che evidenzia il calcolo della progressione geometrica:
e la tabella, completa delle diverse unità di misura che cambiano non appena diventano significative, descrive perfettamente il comportamento del nostro foglio di carta.
Ottantotto, allora. Avete mai pensato a quanto fascino risieda in un numero come ottantotto? Già il suono è seducente, perché sembra quasi lo scandire ritmato d’una tromba: e qualche parentela stretta con la musica ce l’ha davvero, perché proprio ottantotto sono i tasti del pianoforte. Ma anche la forma del numero seduce: la cifra “otto” è palindroma in italiano, ed è un po’ palindroma anche graficamente, a volerla leggere dall’alto in basso: un cerchietto sopra un altro cerchietto. E quando la cifra si raddoppia, la simmetria impera, perche “88” sono un quadrato di cerchi, un otto accanto ad un altro otto, certo, ma anche un simbolo d’infinito sopra un altro simbolo d’infinito. E’ davvero una bella soluzione, per un gioco di matematica.
E sono davvero moltissimi, quelli che hanno trovato la risposta “88”, cosa che ci rende davvero difficile attribuire il premio. Scaldiamo l’atmosfera con qualche citazione sparsa: dice ad esempio Andrea Mattei, da quel di Salerno:
- “…quindi per calcolare “n” ossia l’esponente, ossia il numero di piegature, è sufficiente usare la formula:
n=Log2(2.36518*10^25) = 87.61 Dove Log2 è il log in base 2. In definitiva occorrono circa 88 piegature del foglio per arrivare sulla galassia di Andromeda!”
Gli fa eco Elio Sbardella:
- c (velocità della luce nel vuoto) = 299.792.458 m/s
Giorno siderale = 23h 56min 4s = 86.164 s
Anno siderale = 365d 6h 9min 10s = 31.472.010 s
Distanza percorsa dalla luce in un anno siderale = 299.792.458 m/sx31.472.010 s = 9,4350712 x1015 m
Distanza Terra-Andromeda = 9,4350712 x1015 m x 2.500.000 (distanza a.l. Terra-Andromeda)= 2,3587678×1022 m
Distanza Terra-Andromeda [mm] = 2,3587678×1025 mm
Applicando la formula iniziale avremo:
2n x 0,1mm = 2,3587678×1025 mm
2n = 2,3587678×1026
log 2n = log 2,3587678×1026
n x log 2 = log 2,3587678 x 1026
n x 0,30103 = 26,372685
n = 26,372685 / 0,30103 = 87,60816197 piegature
arrotondando si ha: soluzione = 88 piegature
La soluzione di Elio si preoccupa di valutare puntualmente anche la misura dell’anno luce, e lo fa assumendo come “anno base” per il calcolo l’anno siderale. La cosa può apparire sciocca, ma non lo è affatto: per quanto sia chiarissimo cosa si intenda con “anno luce” (la distanza percorsa dalla luce in un anno), è curioso come in realtà glu uomini non siano ancora tutti d’accordo nel definire il concetto di anno. Usualmente si considera, per il calcolo dell’anno luce, una sorta di anno “standard” formato da 365,25 giorni di 86400 secondi ognuno, cosa che genererebbe un anno luce pari a 9.460.730.472.580.800 metri, ma questa non è l’unica maniera che si trova in letteratura.
La stessa preoccupazione è all’origine dell’attenta soluzione di Fabio Fabbri:
- Per arrivare al risultato, prima calcolerò la distanza di Andromeda in decimi di millimetro, poi userò il logaritmo in base 2 per capire quante volte dovrò piegare il foglio da 0.1 millimetri per arrivare ad Andromeda. Per prima cosa calcolo quanti giorni ci sono in media in un anno. Secondo le regole del nostro calendario, gli anni durano 365 giorni, ma ogni 4 anni c’è un anno bisestile con un giorno in più. Però ogni 100 anni viene fissato un anno non bisestile, che secondo la regola precedente sarebbe dovuto risultare bisestile; Inoltre ogni 400 anni, come eccezione dell’eccezione, uno degli anni che secondo la regola precedente non risulterebbe bisestile, viene comunque fissato bisestile. Quindi la media dei giorni in un anno è:((365*4+1)*100-3)/400=365,2425.
(…) Ora posso calcolare i decimi di millimetro che ci separano da Andromeda. Secondo la mia calcolatrice scientifica, con la precisione di 10 cifre decimali, questa distanza è pari a (7,889238*1013)*299.792.458*10000=2,365134052*1026. Usando il logaritmo, posso calcolare l’esponente da dare a 2 per ottenere questa distanza. Siccome la mia calcolatrice non fornisce direttamente un modo per calcolare il logaritmo in base 2, uso la regola dei logaritmi per la conversione della base usando il logaritmo in base 10 log(2,365134052*1026)/log(2)=87,61205242
Quindi, ipoteticamente, piegando un foglio di 0,1 millimetri su se stesso 88 volte, avremmo un foglio spesso circa 3,3 milioni di anni luce, con cui si potrebbe raggiungere e superare la Galassia di Andromeda. Trovare un foglio abbastanza grande, riuscire a piegarlo su se stesso almeno 87 volte, in modo da ottenere un foglio alto circa 1,63 milioni di anni luce, riuscire a mantenere in ognuno dei 2^87 strati almeno due colonne di molecole alte 0,1 millimetri, in modo da poter piegare il tutto almeno un’altra volta, è lasciato come esercizio al lettore. N.B.: Secondo la Wikipedia in Inglese (http://en.wikipedia.org/wiki/Atom) si stima ci siano circa 2^80 atomi nell’universo osservabile…)
Ma, lo avevamo anticipato, raccontare tutte le soluzioni è davvero impossibile: ci piace segnalare, per qualche ragione che non staremo a raccontare, le soluzioni di Piergiorgio Ferrante, Pierangelo Bellini (anche lui danzante tra logaritmi in base 2 e in base 10),Mario Furlan, Marco Galluccio, Ivo Riccardi (che ha originalmente fatto un “conto alla rovescia”, dimezzando via via la distanza totale), Guglielmo Fulvi, Fabio Guerceri (che ha ricalcolato con maggior precisione la distanza di M31), Claudio Ciaglia.
E naturalmente il vincitore: non ci vergogniamo, per una volta, di confessare di esserci affidati alla sorte, per scegliere il nome del vincitore tra le tutte le soluzioni (esatte) ricevute. E la sorte ha baciato Paolo Borla. A lui va il premio, e le nostre congratulazioni.