Casual Grand Tour

L’evento era speciale, per chi come noi ha due mani e cinque dita per mano.
Il “dieci”, come numero magico e basilare ci accompagna dalla nascita (il che dimostra, una volta per tutte, che delle dita dei piedi non sappiamo ancora cosa farcene) e arrivare al “dieci volte dieci” è necessariamente un traguardo importante. Poi, noi possiamo anche mettere su la nostra celebre aria snob, dire che una base è solo una base, che la base dodici sarebbe certo preferibile, o che il futuro è tutto per la base due, regina dell’informatica: ma sarebbe sempre e soltanto fiato sprecato. Il “10” e le sue potenze non mollano il loro fascino per simili ragioni pratiche e razionali.

Ma alla fin fine, cento è cento a causa del dieci, e dieci è tale perchè abbiamo due mani da cinque dita.
E cinque erano le domande che cercavano risposta….

Domanda numero Uno – Grand Tour tra dodici pianeti

Per una volta, vi raccontiamo anche come sono nati i due problemi.
Un nostro amico qualche giorno prima aveva acquistato un iPod “shuffle” che, come dovreste sapere, esegue le canzoni registrate in sequenza casuale. Si è quindi rivolto agli unici matematici che conosceva per avere la risposta a due imbarazzanti domande:
“Se ho D canzoni caricate, quante canzoni dovrò ascoltare per avere la ragionevole certezza di averle sentite tutte? E dopo quante dovrei aspettarmi di avere una ripetizione?” Il nostro lavoro (a parte risolvere il problema per nostro amico) si è risolto nel trasformare le due domande in problemi specifici: D=12 per il Casual Grand Tour eD=100 per il Numero Preferito.

Cosa dite? Che allora, anziché due problemi, è come se ne avessimo impostato uno solo? Beh, queste sono cose che capitano spesso, in matematica. Tra l’altro, se avete un figlio o un fratellino che colleziona ovetti sorpresa alla ricerca di dieci personaggi d’una serie, potete divertirvi a calcolare quanti ovetti dovete aspettarvi di comprare per completare la serie, semplicemente ponendo D=10. Comodo, no?
Consideriamo allora le probabilità che abbiamo, ad ogni passaggio del Casual Grand Tour, di finire su un pianeta non ancora esplorato; il numero atteso di “salti” per terminarlo sarà pari alla somma degli inversi di queste probabilità. Per semplicità, visto il numero dei pianeti, esprimiamo i valori in dodicesimi.
Al momento del primo “salto”, abbiamo la certezza di finire su un pianeta nuovo, quindi il valore atteso per finire su un nuovo pianeta sarà 12/12 (ovvero 1, la “certezza”). Al secondo passaggio, avremo 1/12 di probabilità di finire sul pianeta già visitato (ossia di restare sullo stesso pianeta, salto nullo) e 11/12 di probabilità di finire su un nuovo pianeta; il numero atteso di viaggi per trovare un nuovo pianeta sarà quindi 12/11.
Per il terzo passaggio, la probabilità di finire su un pianeta già visitato (che ora sono due) sarà 2/12 mentre quella di finire su un nuovo pianeta 10/12, quindi abbiamo un valore atteso (come sempre espresso in “viaggi”) a questo passaggio di 12/10.
In definitiva, il numero di viaggi risulta:

e questo porta ad un valore finale poco maggiore di 37. Ciò detto, vediamo come hanno reagito i solutori: ed è cosa curiosa, perchè abbiamo avuto un margine vastissimo di possibilità. Si va dal minimo possibile (12) ad un massimo di più di 10¹². La migliore approssimazione è stata un 77, ma è particolarmente divertente vedere che il “dodici”, che in pratica è l’unico dato numerico del problema, sia stato usato sia come soluzione diretta, sia come “esponente della soluzione”.

Domanda numero Due – In coda dal Direttore

Anche questa domanda è di natura probabilistica, e anche questa ha mostrato che non c’è troppo feeling tra i lettori di Coelum e la Teoria delle Probabilità. In fondo, sembra essere un male comune, se è vero che un sondaggio in Germania sulla mera interpretazione delle percentuali ha dato risultati scoraggianti.
(Per i curiosi, la domanda era semplicemente questa: “Il valore 40% significa: a) Un quarto. b) Quattro su dieci. c) Uno su quaranta.” Ha dato risposte sbagliate un intervistato su tre.)

Nel caso in esame, comunque, dovrebbe essere evidente che “il numero di Coelum più bello” è una variabile del tutto imprevedibile, non esiste una strategia per cercare di indovinarlo: serve proprio e soltanto come segnatore. In altri termini, è come dire che, da un’urna contenente 100 numeri si comincia ad estrarre un numero, lo si legge, poi lo si rimette nell’urna e si procede ad un’altra estrazione. Ad un certo punto si avrà la prima “ripetizione”, ma non conta affatto “quale” sia il numero ripetuto. Conta invece capire quando è più probabile che tale “ripetizione” appaia per la prima volta. Tanto per fare una scrematura di massima, è evidente che la ripetizione ha probabilità pari a zero quando si estrae il primo numero (non può esserci ancora ripetizione); ha probabilità pari a 1/100 quando si procede alla seconda estrazione (nel caso fortunato in cui si estragga per secondo lo stesso numero già estratto alla prima estrazione; poi 2/100, e così via… Ma quel “così” via è rischioso: è sì evidente che se si arrivasse a fare la centounesima estrazione, si avrebbe a quel punto la certezza che l’estrazione in questione sarebbe una ripetizione, ma è una certezza che si paga assai cara, perchè richiede l’ipotesi, quasi impossibile dal punta di visto probabilistico, che le prime cento estrazioni abbiano prodotto tutti numeri diversi. Insomma, le maggioro probabilità di “vittoria” si hanno posizionandosi “non troppo presto in coda”, perchè sennò i possibili numeri da “ripetere” sono troppo pochi, ma neanche “troppo tardi in coda”, perchè sennò le probabilità che la “ripetizione” avvenga prima del nostro turno è troppo alta. Come accennato poco sopra, è anche di fatto lo stesso problema del Casual Grand Tour, anche se varia il dato numerico e il tipo di domanda. I calcoli sono però più complicati: del resto, ve l’avevamo detto che ci avviavamo “lentamente” verso il direttore…

Sia P(k) la probabilità che il k-esimo della fila vinca; questo significa, tra l’altro, che i primi (k-1) della fila davanti a lui hanno scelto numeri diversi.

Sia inoltre Q(k) la probabilità che i primi k abbiano scelto numeri diversi; questo vuol dire che nessuno dei primi k vince. Deve essere:

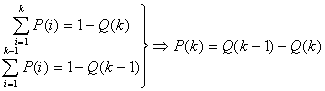
Sia allora D il numero di riviste uscite; se i primi (k-1) hanno scelto numeri diversi, allora per la k-esima persona si ha che la probabilità di vincere è :

P(vincere) = (k-1)/D, mentre quella di “non vincere”, è la complementare P(-vincere) = (D-k+1)/D.

Questo secondo caso significa che si sono generati k scelte diverse; allora deve essere:

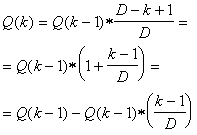
Si noti che dalla prima di questo gruppo si ottiene anche

Mentre dall’ultima:

Sostituendo, si ottiene:

sostituendo k=i+1, si ha:

Da cui:

Il massimo di questa funzione risulta essere quello per cui:

Ossia:

Da cui, per D=100, si ottiene un valore di x maggiore di 10, e quindi ci mettiamo inundicesima posizione.

I solutori, qui, hanno nuovamente mostrato qualche difficoltà: se Damiano Della Grotta e Pierangelo Bellini hanno quantomeno mostrato di aver ben compreso quali siano le due “forze contrapposte” che spingono una verso l’inizio, l’altra verso la fine della coda, non c’è stata sufficiente quantificazione per arrivare ad una ipotesi credibile. Chi invece ha risposto dando come ottimali posizioni come la prima, la seconda, l’ultima o la penultima, non ha probabilmente colto per intero lo spirito del problema..

Domanda numero Tre – Cento con le Nove Cifre

Qui, qualche soluzione buona la abbiamo ottenuta. Ad esempio, questa di Marco Valentino:

1×2+3×4-5×6-7+8+9=100

o anche questa di Damiano Della Grotta:

1+2+3-4×5-6+7+8-9×10=100

Solo un piccolo commento a margine: Marco ha usato le nove cifre, Damiano i primi dieci interi. Comunque entrambe le soluzioni vanno lette non come le care vecchie espressioni scolastiche (quelle in cui era necessario risolvere prima moltiplicazioni e divisioni, e solo dopo addizioni e sottrazioni), perchè così facendo di ottengono risultati ben diversi da cento. Le stringhe vanno proprio lette “sequenzialmente”.

Come a dire che per risolvere 1×2+3×4 non si deve fare

(1×2)+(3×4)=2+12=14,

ma

(((1×2)+3)x4)=((2+3)x4)=(5×4)=20

Domanda numero Quattro – Il Dodici è tondo

Base 1: 111111111111
Base 2: 1100
Base 3: 110
Base 4: 30
Base 5: 22
Base 6: 20
Base 7: 15
Base 8: 14
Base 9: 13
Base 10: 12
Base 11: 11
Base 12: 10

Ok, non resta che scegliere voi stessi le basi per le quali dodici è sufficientemente “tondo” (ad esempio, 2, 3, 4, 6, 12, ma in fondo è una questione di gusti…)

Domanda numero Cinque – I Cento e i Dodici (nascosti)

Orbene, non vorremmo annoiarvi elencandovi puntualmente tutti i punti dove sono comparse le parole in questione.

Però, tanto per andare sul sicuro, avete notato cosa formano le lettere iniziali dei paragrafi (che abbiamo avuto cura di evidenziare in neretto)? Pierangelo Bellini lo ha notato, ma quanti altri?