Siamo sicuri che qualche volta è capitato anche a voi.
Per forza, via, siamo umani, in fondo… E’ quasi certo che anche voi abbiate “sbagliato” ad esporre un problema, un testo, qualcosa. A noi è capitato in questa occasione, quando, raccontando di come i nostri scienziati sparpagliati per il Sistema Solare riuscissero a scambiarsi i campioni geologici, ci siamo brillantemente scordati di specificare che uno spazio-porto può contenere una sola spazio-nave alla volta. Del resto, come dicevamo nel riquadro delle soluzioni pubblicato su Coelum 104, “uno spazio-porto può ospitare una sola spazio-sonda alla volta (ma non era evidente dalle normali regole di spazio-navigazione? Ma chi vi ha dato la spazio-patente, si può sapere?)”.
Senza questo piccolo ma fondamentale vincolo, esistono chiaramente delle soluzioni scorciatoia. Ci fa notare ad esempio Marco Valentino che:
- “basta che le spedizioni di 10 pianeti partano contemporaneamente verso un unico pianeta, così da ripartire con tutti i campioni (impiegando un solo mese)”.
In maniera non meno diretta ed esplicita, anche Fabio Fabbri mette in evidenza che:
- “… si può scegliere un pianeta base. Ognuno degli altri pianeti invierà la propria navetta verso il pianeta base, con un carico di 10 campioni.Da ogni navetta verrà scaricato un campione per il pianeta base, si caricherà un campione del pianeta base e si faranno degli scambi tra navette in modo che ogni navetta abbia un campione dalle altre navette. Così le navette ripartiranno per il pianeta di origine con i 10 campioni dagli altri pianeti, terminando in 2 mesi. La generalizzazione è banale:se ci sono n pianeti basta caricare ogni navetta con n-1 campioni.”
In realtà, come lo stesso Fabio e molti altri avevano subodorato, il problema richiedeva qualche difficoltà maggiore. Ed è stato piacevole vedere come molte persone si siano autonomamente sforzate di comprendere cosa davvero si celasse “…sotto il velame de li versi strani” di dantesca memoria.
Un affezionato lettore di questa rubrica ci ha letteralmente lasciato a bocca aperta per la sua capacità di mescolare sapientemente arte e logistica astronavale. Si tratta del solito Pierangelo Bellini, che ci ha inviato questo gioiello:
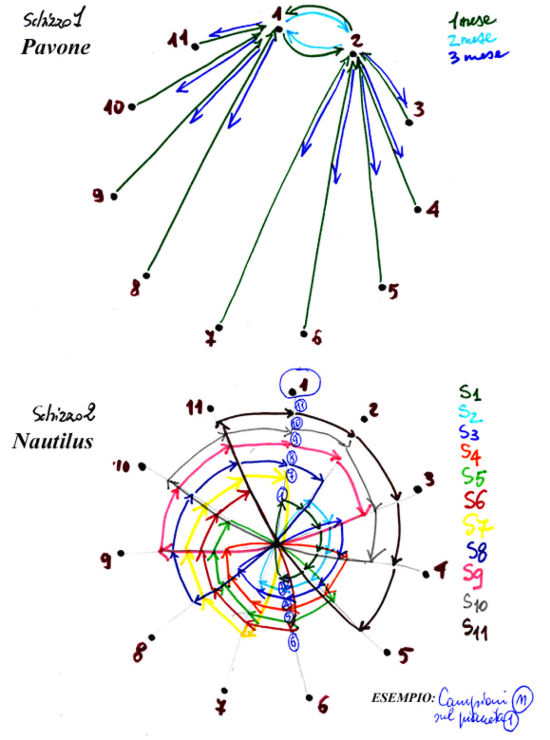
- “Numerando da 1 a 11 i pianeti, le rispettive sonde e i corrispondenti campioni, ho organizzato due punti di raccolta e scambio di campioni, sui pianeti 1 e 2 (cfr. schizzo 1). Le sonde 3, 4, 5, 6 e 7, con un viaggio di un mese si recano sul P2 (pianeta 2 o punto raccolta 2), mentre le sonde 8, 9, 10 e 11 vanno contemporaneamente su P1. Le sonde S1 e S2 dei rispettivi pianeti P1 e P2 invece vanno, reciprocamente, sul pianeta vicino: S1 su P2 e S2 su P1.
Tutte le sonde scaricano set di campioni relativi al loro pianeta ; perciò su P1, dopo 1 mese, troviamo i campioni C2, C8, C9, C10, C11 e C12 (oltre naturalmente C1), mentre su P2 ci sono i campioni C1, C3, C4, C5, C6 e C7 (oltre naturalmente C2).
Il secondo mese , mentre tutte le altre sonde stanno ferme in manutenzione, le sonde S1 e S2 ritornano con tutti i tipi di campioni presenti sul punto/pianeta di raccolta , alla propria base di partenza . Dunque, dopo 2 mesi, sia su P1 che su P2 sono immagazzinati tipi di campioni di ogni pianeta del sistema, Terra esclusa.
Ogni sonda, tranne la 1 e la 2 che restano a casa, prende un esemplare dei campioni di ciascun pianeta e col carico completo , se ne torna al pianeta natio in un mese di viaggio.
Dopo 3 mesi dunque ciascun pianeta ha, almeno, 1 campione per ciascun pianeta.
(…)
Per curiosità, invio anche una seconda soluzione che mi piace di più, è semplice e suggestiva e somiglia alla quadriglia o alla crescita della conchiglia di un Nautilus, ma necessita di 6 mesi di viaggio (cfr. schizzo 2).
Ogni sonda parte dal suo pianeta (es.:1) e si reca sul consecutivo (2) depositando il campione del proprio pianeta (c1) e prelevando un campione del pianeta che lo ospita (C2); questo per 5 mesi.
Nel frattempo le altre sonde fanno altrettanto, come se si inseguissero. Dopo 5 mesi quindi ogni sonda ha nella stiva 5 tipi di campioni diversi, avendo distribuito il proprio tipo su 5 pianeti . Nel sesto mese ciascuna sonda torna a casa e vi trova, scaricati dalle sonde ivi transitate, altri 5 tipi, ancora diversi, di campioni. Questi, sommati ai 5 che ha nella stiva e a quello ‘residente’ del proprio pianeta fanno 11 campioni diversi.
Calcoli a parte, quel che troviamo davvero incantevoli sono gli schizzi citati nel testo.
Una bella ed esaustiva analisi ce l’ha fornita anche Massimo Andreolli, che attentamente esamina anche il criterio di “ottimizzazione”; non è infatti un elemento trascurabile, perché quando si a che fare con i numeri interi (e con i pianeti – normali o nani che siano – ancora quelli bisogna usare…) si hanno spesso sorprese in questo senso. In ogni caso, l’affermazione più notevole di Massimo resta quella che ha posto in apertura alla sua mail:
- “… sono quello che non aveva tempo per scrivere la dimostrazione del teorema di Fermat”
Bene, ma alla fin fine, chi ha vinto, questo mese? Ha vinto il già citato Fabio Fabbri, anche per la perseveranza dimostrata. Informato del fatto che la limitazione negli spazioporti c’era ed era attiva, non si è perso d’animo ed ha scodellato una soluzione più elaborata, dove dice, tra l’altro:
- “Con la specifica del vincolo che su un pianeta può arrivare una sola sonda per volta e ripartire prima che ne arrivino altre, il problema si fa più interessante.
Comunque, essendo un programmatore abituato a ragionare con algoritmi, numeri binari e potenze di 2, non ho fatto molta fatica a trovare una soluzione alternativa, anzi due. Una si basa sempre sulla scelta di un pianeta base, ma con partenze e arrivi non contemporanei, l’altra soluzione muove le astronavi in base ad un algoritmo che porta su ogni pianeta prima 1, poi 3, poi 7 campioni dagli altri pianeti, con crescita esponenziale. A seconda dei casi, può essere migliore la prima o la seconda soluzione.
La prima soluzione prevede sempre la scelta di un pianeta base. Ipotizzando che su un pianeta vi può essere solo una navetta alla volta che scarica e carica in un tempo t, ignorando quello che farà la navetta del pianeta base, le altre astronavi partiranno dai loro pianeti verso il pianeta base una alla volta, e ognuna attenderà che sia passato un tempo t dal lancio precedente prima di partire. Se i pianeti sono N, si caricano su ogni navetta N-1 campioni, e ogni navetta al proprio turno partirà, depositerà i campioni sul pianeta base e tornerà al proprio pianeta.
Quando l’ultima navetta arriverà sul pianeta base, dopo aver scaricato i campioni dell’ultimo pianeta, si carica un campione del pianeta base e N-2 campioni provenienti dagli altri pianeti (uno per pianeta), per poi tornare sull’ultimo pianeta. Ora le altre navette (dalla prima alla penultima) devono tornare sul pianeta base per caricare i campioni provenienti dagli altri pianeti, e portarli sul rispettivo pianeta.
Indicato con m la durata del viaggio della navetta (nel problema posto equivale a un mese), se 2m+2t > t*N (risolvendo t<(2m)/(N-2)), quando l’ultima navetta è partita dal proprio pianeta ed è passato un tempo t, la prima non è ancora tornata al pianeta d’origine. In questo caso, appena la prima navetta torna sul proprio pianeta, dovrà ripartire per tornare sul pianeta base. Se i tempi di carico/scarico sono molto lunghi e/o se il numero dei pianeti è molto alto, può capitare che la prima navetta sia già tornata a destinazione mentre l’ultima deve ancora partire. In questo caso la prima navetta dovrà aspettare che l’ultima sia partita dal proprio pianeta, attendere un ulteriore tempo t e partire per il pianeta base. Successivamente, le navette dalla seconda alla penultima torneranno sul pianeta base partendo una alla volta attendendo un tempo t dal lancio precedente prima di poter ripartire.
Queste navette, una volta sul pianeta base, caricheranno N-1 campioni: uno per pianeta compreso il pianeta base ed escluso il proprio. Così potranno portarli sul proprio pianeta e compiere la missione.
Il tempo totale richiesto è definito partendo dal tempo richiesto per il primo lancio (andata e ritorno) o dal tempo di attesa richiesto per poter compiere il lancio della navetta sull’ultimo pianeta, a seconda di qual è il maggiore. Nel primo caso il tempo richiesto è 2m+2t(due viaggi più due soste); altrimenti è N*t (la prima navetta per ripartire deve attendere che tutte le altre siano già partite). Una volta ripartita la prima navetta, vi saranno altre N-2 pause di durata t prima che la navetta del penultimo pianeta possa partire, impiegando m+t+m per completare il giro. Riassumendo, la formula per il calcolo del tempo richiesto è MAX[(2m+2t),(N*t)] + 2m + (N-1) * t.
Volendo migliorare questa soluzione, si può usare la navetta sul pianeta base e la navetta sull’ultimo pianeta (che altrimenti starebbe ferma per circa due mesi) per anticipare il completamento della distribuzione sul penultimo e sul terzultimo pianeta. Comunque questa finezza non dovrebbe ridurre significativamente il tempo richiesto: sarà comunque necessario un tempo di almeno 4m, al massimo si può riuscire a ridurre un poco il coefficiente di t.
Nella seconda soluzione, bisogna etichettare i pianeti assegnando ad ognuno un indice da 0 a N-1. Inoltre bisogna calcolare k, che sarà un intero pari a log2(N) arrotondato per eccesso.
Per semplificare la spiegazione, userò l’operazione “modulo”, molto usata dai programmatori. Calcola il resto della divisione tra numeri interi e di solito viene indicata con %. Ad esempio 1%3=1, 3%3=0, 5%3=2, 6%3=0 e così via. Inoltre indicherò con i l’indice del pianeta su cui si trova una navetta al passo corrente Al passo 1, si carica su ogni navetta 2^(k-1) campioni del proprio pianeta d’origine. Ogni navetta parte per il pianeta con indice (i+1)%N.
Al passo 2, da ogni navetta si scaricano 2^(k-2) campioni del pianeta d’origine, e si caricano altrettanti campioni del pianeta corrente. Ogni navetta partirà per il pianeta (i+2)%N.
Al passo 3, si scaricano da ogni navetta 2^(k-3) campioni del pianeta d’origine e altrettanti campioni del pianeta visitato precedentemente.
Vengono caricati 2^(k-3) campioni del pianeta corrente i e altrettanti campioni provenienti da i-1 (metà dei campioni lasciati dalla navetta che ha visitato il pianeta al passo precedente). Alla fine di questo passo, la navetta conterrà 2^(k-1) campioni provenienti da 4 pianeti diversi (sono 2^(k-3) per ogni pianeta), e li porterà sul pianeta con indice (i+4)%N, che non ha ancora visto alcun campione proveniente da questi pianeti.
Nei successivi passi p, si scaricano 2^(k-p) campioni per ciascun gruppo di campioni provenienti da pianeti diversi, e si caricano 2^(k-p) campioni del pianeta corrente. Per ogni gruppo di campioni provenienti da altri pianeti portati dalle navette precedenti e presenti sul pianeta corrente, si caricano 2^(k-p) esemplari, cioè la metà. La navetta conterrà sempre 2^(k-1) campioni, provenienti da 2^(p-1) pianeti diversi. La navetta partirà alla volta del pianeta (i+(2^(p-1)))%N.
Questo continua fino al passo k. A quel punto la navetta conterà campioni provenienti da 2^(k-2) pianeti diversi e per ognuno di questi avrà due campioni. Verrà depositato un campione per gruppo. Inoltre viene caricato un campione del pianeta corrente e un campione per ognuno dei 2^(k-2)-1 gruppi di campioni provenienti da altri pianeti portati dalle navette precedenti (all’ultimo passo i gruppi sono composti da due elementi). Ora la nave è caricata con 2^(k-1) campioni, ognuno proveniente da un pianeta diverso, e si dirigerà verso il pianeta (i+(2^(k-1)))%N per il viaggio conclusivo. Quando le navette saranno arrivate a destinazione, su ogni pianeta ci sarà almeno un campione proveniente da ognuno degli altri pianeti, e la missione sarà compiuta.
Il tempo impiegato sarà (m+t)*k = (m+t)*sup(log2(N))
Se k<=4 => N<=16, la soluzione migliore è la seconda. Per un numero maggiore di pianeti, in certi casi, la prima soluzione può essere migliore, a seconda del tempo di carico/scarico.
E con questo Fabio si è aggiudicato il premio messo in palio. Ma non scoraggiatevi: se vi sembra che la sua soluzione sia ulteriormente ottimizzabile fatecelo sapere, e vedremo cosa si può fare…