 Soluzione, considerazioni e approfondimenti suggeriti sul quesito posto da Paolo Alessandrini nella rubrica Moebius pubblicata su Coelum 178 di febbraio.
Soluzione, considerazioni e approfondimenti suggeriti sul quesito posto da Paolo Alessandrini nella rubrica Moebius pubblicata su Coelum 178 di febbraio.
Conigli e fiori
Nella storia della scienza, e in particolare della matematica, vi sono due giganti pisani. Uno è famosissimo: Galileo Galilei, da tutti conosciuto come il padre della scienza moderna. L’altro, invece, non è così noto: eppure la sua importanza nelle vicende della matematica è enorme.
Pisano lo era di fatto, ma anche di nome: si chiamava infatti Leonardo Pisano, ma dato che suo padre era Guglielmo dei Bonacci, venne soprannominato Fibonacci, cioè “figlio del Bonacci”.

Il padre Guglielmo era un ricco mercante: aveva fatto fortuna tessendo relazioni commerciali con la città algerina di Bugia. Il giovane Fibonacci trascorse anche lui alcuni anni in Africa, dove venne a contatto con molte tecniche matematiche note nel mondo arabo e ancora sconosciute in Occidente. Fibonacci, che per anni continuò a viaggiare aiutando il padre nelle sue attività commerciali, cominciò ad approfondire in modo originale queste conoscenze matematiche, e ben presto la sua occupazione di mercante passò in secondo piano, soppiantata dal forte interesse per la matematica.
L’imperatore Federico II, famoso per la sua sensibilità culturale e per suo amore per la scienza, venne a conoscenza dei promettenti studi matematici di Fibonacci e gli offrì un vitalizio, che gli permise di dedicarsi completamente ai suoi studi.
Nel 1202 Fibonacci pubblicò la sua opera più importante, il Liber Abbaci, nella quale, oltre a numerosi altri fondamentali concetti di aritmetica e algebra, introdusse per la prima volta in Europa il sistema di numerazione decimale, basato sull’uso delle cosiddette cifre “arabe”, tuttora in uso, compreso lo zero. A quel tempo in Europa si usavano i numeri romani e lo zero era del tutto sconosciuto: non stupisce il fatto che la diffusione del nuovo sistema proposto da Fibonacci incontrò all’inizio molti ostacoli (molti ritenevano che lo zero provocasse confusione e venisse impiegato anche per mandare messaggi segreti).

Nel Liber Abbaci Fibonacci introdusse anche la successione di numeri che prende il suo nome, e che era per la verità già nota agli arabi.
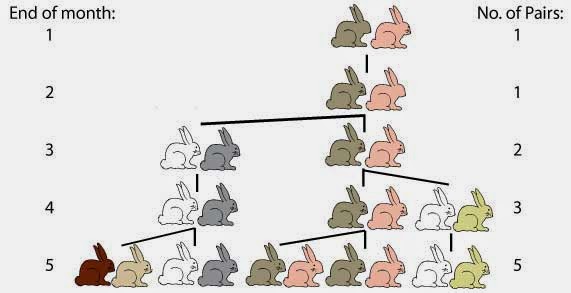
Fibonacci fu un geniale matematico teorico, uno dei più grandi di sempre, ma non rinnegò mai il suo “background” di mercante pragmatico e concreto. Il suo interesse per la successione che porta il suo nome era legato ad un’utilità pratica: in particolare Fibonacci si era accorto che la crescita di una popolazione di conigli poteva essere rappresentato con buona precisione dai numeri della successione.
Immaginiamo di avere, al primo mese, due giovani conigli. Nel secondo mese saranno diventati adulti, e come tali potranno avere figli. Nel terzo mese nascerà una seconda coppia di conigli, ad esempio maschio e femmina. Nel quarto mese la prima coppia genererà altri due conigli, mentre la seconda coppia avrà raggiunto la maturità. Ancora un mese, e le due coppie adulte genereranno altrettante coppie di figli, e l’altra coppia diventerà adulta.
Come rappresentare matematicamente questa crescita della popolazione nei mesi successivi? Semplice: attraverso la sequenza 1, 1, 2, 3, 5, 8, 13, 21, 34, 55…., nella quale ogni numero è la somma dei due precedenti.
Questi numeri godono di una enorme quantità di proprietà aritmetiche. Tanto per dirne una, prendete tre numeri di Fibonacci consecutivi, e moltiplicate il primo per il terzo e il secondo per se stesso: otterrete sempre due numeri interi tra di loro consecutivi. Provate ad esempio con i numeri di Fibonacci 5, 8 e 13: ebbene, 5 x 13 fa 65, mentre 8 x 8 fa 64, e ovviamente 65 e 64 sono numeri consecutivi.
Un’altra bizzarra proprietà: se sommiamo tra loro 10 termini consecutivi della successione di Fibonacci, otteniamo sempre un multiplo di 11.
E ancora: ogni numero di Fibonacci è uguale alla somma dei numeri di Fibonacci che lo precedono eccetto l’ultimo, aumentata di 1.
E abbiamo appena scalfito la superficie.
I numeri di Fibonacci si ritrovano inoltre in moltissimi fenomeni naturali. E’ sorprendente, ad esempio, riscontrare che molti fiori hanno un numero di petali che appartiene alla successione di Fibonacci: ad esempio i gigli hanno tre petali, i ranuncoli hanno cinque petali, le margherite solitamente 34 o 55 oppure 89.
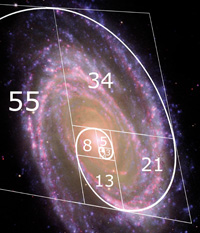
Le infiorescenze presenti al centro del girasole descrivono spirali concentriche, alcune delle quali sono disposte in senso orario e altre in senso antiorario: se si conta il numero di spirali orarie e di spirali antiorarie, si ottengono due numeri di Fibonacci consecutivi, ad esempio 21 e 34, oppure 34 e 55.
Fibonacci si ritrova nel mondo delle piante in molti altri casi: dalla disposizione dei rami di alcuni alberi, alla forma delle foglie, ai pistilli sulle corolle dei fiori, alla conformazione degli ananas e delle pigne di alcune conifere.
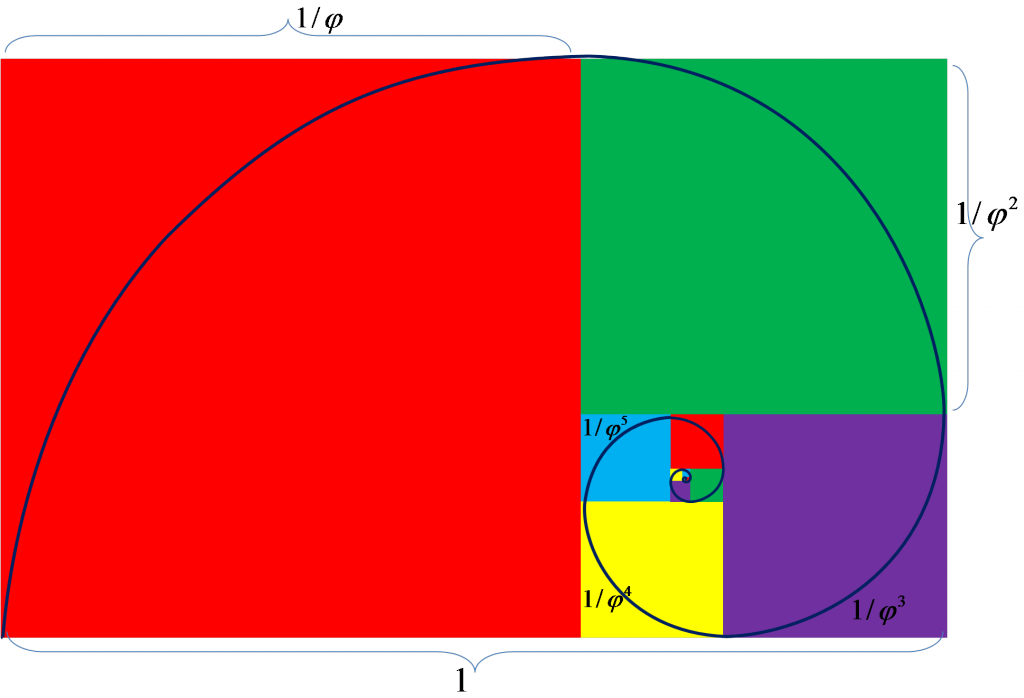
Ma una delle peculiarità più notevoli dei numeri di Fibonacci è legata ad un concetto familiare anche ai matematici antichi: la cosiddetta sezione aurea, da sempre associata ad un ideale di perfezione e di armonia.
Prendiamo un pezzo di spago di una certa lunghezza, e decidiamolo di tagliarlo in due pezzi, uno più lungo e uno più corto. Vogliamo però che la lunghezza totale dello spago originario stia a quella del pezzo lungo come la lunghezza del pezzo lungo sta a quella del pezzo corto. C’è un modo per ottenere questo? Sì, e se riusciamo ad effettuare questo taglio, possiamo dire che le lunghezze dei pezzi che otteniamo stanno tra loro in un rapporto di sezione aurea.
Per la precisione, il rapporto tra le due lunghezze sarà uguale a circa 1,618: fin dall’antichità questo numero (φ) è stato chiamato con nomi altisonanti, come sezione divina, proporzione aurea, numero di Fidia, e così via.
Ma che c’entrano i numeri di Fibonacci? Il primo ad accorgersi di uno speciale legame tra questi due concetti matematici fu Keplero, nel 1611. Se si prende un qualsiasi numero della successione di Fibonacci, e lo si divide per il numero che lo precede, si ottiene un numero che è abbastanza vicino al rapporto aureo; facendo questo esperimento con numeri che si trovano molto avanti nella successione, quindi numeri molto grandi, il rapporto si avvicina sempre di più a quel fatidico 1,618.
I numeri di Fibonacci e la sezione aurea si ritrovano spesso anche nella musica.
Molti compositori soprattutto nel Novecento, hanno costruito le loro composizioni applicando questi concetti matematici alle durate temporali dei brani, o al numero di misure, di battute o di note musicali: ad esempio Bela Bartok li ha utilizzati per la sua celebre Musica per archi, percussioni e celesta, Claude Debussy per la composizione Riflessi nell’acqua, e ancora Igor Stravinsky, Karl Heinz Stockhausen, Luigi Nono e György Ligeti.
Nel mondo del rock, possiamo citare i Genesis (in Firth of fifth), i Deep Purple (in Child of time), i Dream Theater (in Octavarium), i Tool (in Lateralus).
L’enigma
Il quesito fibonacciano pubblicato su Coelum 178 era, in sintesi, il seguente.
Nell’arco di 12 ore, quante galassie è possibile informare?
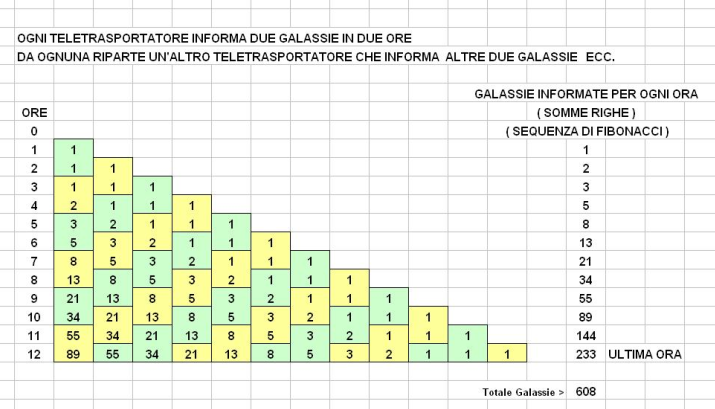
La risposta è perfettamente e chiarissimamente illustrata nella figura seguente, inviataci da Daniele Tosalli, uno dei lettori che ha saputo risolvere l’enigma.
Nella prima ora una galassia sarà raggiunta dal primo viaggiatore. Nella seconda ora lo stesso viaggiatore raggiungerà una nuova galassia, mentre un nuovo messaggero partirà alla volta di una terza galassia. Nel corso della terza ora altre tre galassie potranno essere avvisate della terribile minaccia, e così via.
In generale, si vede facilmente che il numero di galassie raggiunte nella N-esima ora corrisponde all’N-esimo numero della sequenza di Fibonacci.
Per calcolare il numero complessivo di galassia informate nel corso di dodici ore, si devono quindi sommare i primi 12 numeri di Fibonacci, eventualmente aggiungendo 1 per tenere conto della galassia d’origine, cioè la nostra Via Lattea.
Le soluzioni dei lettori
A vincere l’abbonamento è stato Daniele Borrè, che per primo ha fornito la soluzione esatta.
Oltre a lui hanno saputo risolvere l’enigma anche il già menzionato Daniele Tosalli, Maurizio Carlino (che, com’è sua abitudine, ha inviato una ammirevole analisi matematica del problema), ed Elio Sbardella (che per errore non era stato citato sulla rivista).
Altri lettori si sono cimentati nel problema ma hanno sbagliato a calcolare la somma dei numeri di Fibonacci; altri ancora hanno indicato il dodicesimo numero di Fibonacci tralasciando di sommare i precedenti.
Complimenti comunque a tutti coloro hanno provato ad affrontare la sfida, e soprattutto a chi ha inviato la risposta esatta.