Good luck, Bad days, Bad numbers

Chissà, forse poi la fortuna esiste davvero. Non è che noi si voglia passare armi e bagagli nel fronte dei superstiziosi, non sia mai! Ma resta il fatto che a parlare di sfortuna non abbiamo fatto un grosso affare. Forse la colpa è delle vacanze, del mare, della poca voglia di provare a risolvere i problemi: fatto sta che le soluzioni al problema del Venerdì 17 sono

state davvero poche. O forse la sfortuna esiste davvero, visto quel che ci ha scritto uno dei solutori più affezionati, Pierangelo Bellini:

Questa volta, non riuscendo ad elaborare formule ed equazioni classiche, deterministiche, ho deciso di affrontare i problemi da un punto di vista meccanico-quantistico , nell’interpretazione più genuina di Copenhagen. Mi spiego: considerando, relativamente alle mie abilità, tutto il sistema “calendariale” come indeterminato, mi sono basato esclusivamente sui risultati delle osservazioni, dell’esperimento. Così ho fatto una tabella con Access e vi ho inserito tutti i dati emersi dagli esperimenti, cioè dalle osservazioni di un bel po’ di… calendari!!!!
Con l’aiuto dell’intuito femminino di mia moglie Tina, ho inferito:
– L’intervallo massimo tra due Venerdì 17 è di 396 giorni, pari a 1 anno più un mese di 31 giorni;
– L’intervallo minimo tra due Venerdì 17 è di 28 giorni, pari all’età di un normale Febbraio;
– La probabilità che un anno inizi di Domenica è uguale a quella che esso inizi di Sabato.
Il perché non lo conosco, almeno non diversamente da come Bohr sapeva perché la meccanica quantistica funziona così bene!
PS : peccato! La letterina precedente, andata persa, era meno frettolosa.

È proprio il post-scriptum a preoccuparci: già le soluzioni arrivate erano poche, se tra queste dobbiamo annoverare anche delle disperse, c’è davvero di che dormire preoccupati. La soluzione di Pierangelo, comunque, non prova a mettere in conto dei calcoli: si basa solo sull’analisi per così dire “statistica” di diversi calendari possibili. Un tentativo migliore, se pure non perfetto dal punto di vista analitico, è quello fatto dal vincitore di questo mese,Maurizio Leotta, che, pur restando sul fronte delle “forza bruta”, tenta quantomeno un’analisi numerica dei dati:

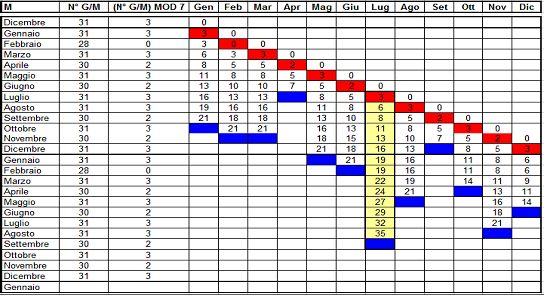
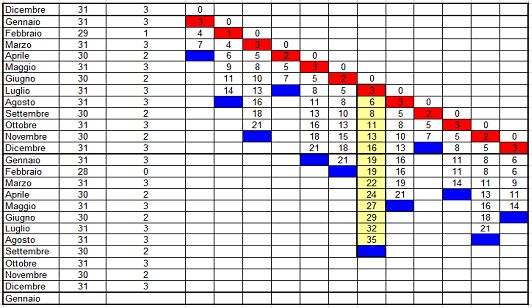
Qual è l’intervallo MASSIMO tra due Venerdì 17? L’intervallo MASSIMO che può presentarsi tra due Venerdì 17 è pari a 427 giorni cioè 61 settimane. Ecco il metodo di calcolo (molto brute force 😉 ) in giallo gli intervalli massimi:
Anni NON BISESTILI: Un giorno del mese rosso si ripete nel mese blu successivo

I Anno Bisestile: Un giorno del mese rosso si ripete nel mese blu successivo

II Anno Bisestile: Un giorno del mese rosso si ripete nel mese blu successivo

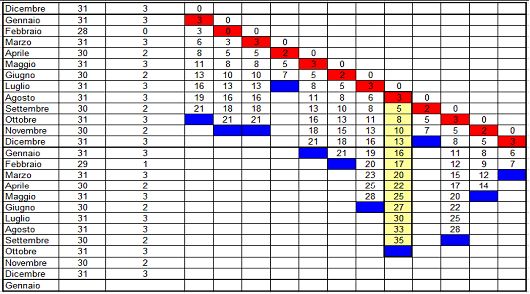
Qual è l’intervallo MINIMO tra due Venerdì 17? L’intervallo MINIMO che può presentarsi tra due Venerdì 17 è pari a 28 giorni, cioè 4 settimane. Questo avviene quando, in anni NON bisestili, si presenta un Venerdì 17 Febbraio seguito quindi da un Venerdì 17 Marzo.
È più probabile che l’anno inizi di Sabato o di Domenica?
È equiprobabile.

Il fatto significativo è che Maurizio ha ben impostato il problema, analizzando le combinazioni possibili tra “tipi di anno: ha cioè notato che l’asimmetria bisestile-non bisestile è eliminabile se si considerano le tre combinazioni possibili; una coppia consecutiva di anni non bisestili, oppure la coppia “bisestile-non bisestile” e infine la “non bisestile-bisestile”. Di qui tutta l’analisi esposta, che poteva firse essere ulteriormente semplificata se si introduceva il concetto di “modulo 7”, perché se assegniamo ai giorni di un anno un numero in modulo 7 a partire dal 17 gennaio, otteniamo per i giorni 17 dei diversi mesi le due serie:

0, 3, 3, 6, 1, 4, 6, 2, 5, 0, 3, 5 per gli anni non bisestili;
0, 3, 4, 0, 2, 5, 0, 3, 6, 1, 4, 6 per gli anni bisestili.

Da cui si vede quasi direttamente la conclusione alla quale giunge Maurizio: ad esempio, negli anni non bisestili il numero più frequente è il 3, che si ripete 3 volte. Se, quindi, il 3 identifica il Venerdì (ossia se il 17 gennaio era un martedì, ossia il primo gennaio una domenica), avremo dei Venerdì 17 nei mesi di febbraio, marzo e novembre (questo è successo, ad esempio, nel 2002). Per quanto riguarda gli anni bisestili, invece, la massima ricorrenza è sul valore 0, quindi avremo il massimo numero di Venerdì 17 se lo 0 corrisponde ad un venerdì, ossia se era Venerdì il 17 gennaio ossia se l’anno (bisestile) cominciava con un mercoledì (succederà, ad esempio, nel 2020).

Per il calcolo dei periodi di “libertà dai venerdì 17”, le tre sequenze biennali introdotte da Maurizio, possiamo vederle composte in questo modo:
1. Due anni non bisestili;
2. Un anno non bisestile seguito da uno bisestile;
3. Un anno bisestile seguito da uno non bisestile.

In questo modo, con lo stesso metodo visto sopra, si generano le sequenze