I dadi di Platone – approfondimenti sul quesito e soluzione

I solidi platonici

Nel numero 184 di Coelum ho parlato di solidi platonici. I solidi che portano il nome del celebre discepolo di Socrate sono dei poliedri: in altre parole, appartengono alla grande famiglia dei solidi delimitati da un numero finito di facce piane poligonali. Non sono però dei poliedri qualsiasi: hanno la caratteristica di avere come facce poligoni regolari, tutti uguali tra di loro, e inoltre hanno tutti i vertici e gli spigoli equivalenti.

Sono, per così dire, l’analogo dei poligoni regolari in versione 3D (non a caso vengono spesso denominati poliedri regolari, o solidi regolari). Ma c’è una differenza sostanziale, e, per così dire, affascinante: mentre i poligoni regolari sono infiniti (per ogni numero intero N esiste un poligono regolare con N lati), i solidi platonici sono solo cinque.

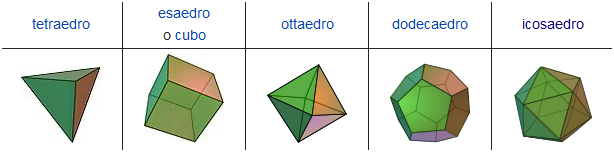
Questi cinque poliedri portano nomi suggestivi, che derivano dal greco: tetraedro, esaedro (o cubo), ottaedro, dodecaedro e icosaedro.

Dato che in greco έδρα significa “base”, è facile comprendere l’etimologia di questi nomi: un tetraedro è un poliedro con 4 facce, un esaedro ne ha 6, un ottaedro 8, un dodecaedro 12 e un icosaedro 20.

.

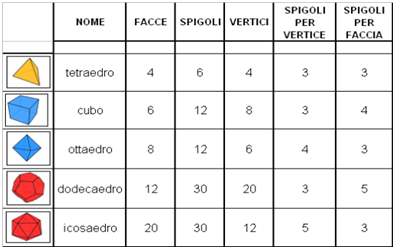
Osservate che ognuno dei solidi regolari può essere convertito nel suo duale: basta trasformare le facce in vertici e i vertici in facce. Sottoposto a questa metamorfosi, il tetraedro resta invariato, avendo 4 facce e 4 vertici. Il cubo, invece, diventa un ottaedro, e viceversa. Il dodecaedro si tramuta in un icosaedro, e così anche all’inverso.

Perché solo cinque?

Perché i solidi platonici sono soltanto cinque? Davvero non ne esistono altri?

Ai tempi di Platone, cioè nel IV secolo a.C., si intuiva già che i solidi regolari fossero cinque, ma nessuno lo aveva ancora dimostrato rigorosamente. Nel suo dialogo “Timeo”, il filosofo ateniese descrisse i solidi regolari, e ne associò quattro agli elementi fondamentali dell’universo: il tetraedro al fuoco, il cubo alla terra, l’ottaedro all’aria, l’icosaedro all’acqua. Il quinto solido, il dodecaedro, venne fatto corrispondere alla forma dell’universo nella sua totalità.

Circa un secolo e mezzo dopo, il grande matematico Euclide riuscì a provare che i solidi regolari sono soltanto i cinque descritti da Platone, e che non ce ne sono altri.

Una dimostrazione intuitiva può essere compresa senza grande sforzo.

Prima di tutto, osserviamo che in un qualsiasi poliedro, ogni vertice è il punto di incontro di almeno tre facce: infatti due facce si possono incontrare su uno spigolo, ma non possono formare un vertice.

Inoltre, queste tre o più facce devono essere poste su piani diversi, perché se giacessero sullo stesso piano formerebbero in realtà una faccia sola, e non tre. Di conseguenza, la somma dei tre o più angoli che si incontrano in un vertice deve essere inferiore a 360°. Infatti, se fosse esattamente 360°, le facce sarebbero sullo stesso piano, mentre una somma angolare più bassa consente al punto di incontro di “alzarsi”, creando un vertice.

Ricordando che le facce del solido devono essere poligoni regolari, vediamo quali possono essere questi poligoni.

Certamente potrebbero essere triangoli equilateri. Ogni angolo di un triangolo equilatero è ampio 60°: quindi in un vertice del solido potrebbero incontrarsi 3 facce triangolari formando un angolo di 3 × 60° = 180° < 360°, oppure 4 facce triangolari formando un angolo di 4 × 60° = 240° < 360°, oppure 5 facce triangolari formando un angolo di 5 × 60° = 300° < 360°. Con 6 facce saremmo invece fuori, perché uscirebbe un angolo di 6 × 60° = 360°: troppo perché il vertice possa “alzarsi”.

Le facce potrebbero anche essere quadrati, in cui ogni angolo è di 90°. In ogni vertice del solido potrebbero infatti convergere 3 facce quadrate, a creare un angolo di 3 × 90° = 270° < 360°: già con 4 facce l’angolo sarebbe di 4 × 90° = 360°, quindi da escludere.

Infine, potremmo utilizzare come facce pentagoni regolari, nei quali ogni angolo è di 108°. Ogni vertice del solido potrebbe essere allora punto di incontro di 3 facce pentagonali, formando un angolo di 3 × 108° = 324° < 360°: con 4 facce saremmo invece oltre i limiti consentiti (4 × 108° = 432° > 360°).

Non potremmo invece utilizzare facce esagonali, perché in un esagono ogni angolo è di 120°, e già 3 facce formerebbero un angolo di 360°, che contribuirebbe a tassellare il piano, senza poter elevare un vertice del solido. Poligoni con più lati sono ancora peggiori, perché con sole 3 facce creerebbero angoli più grandi dell’angolo giro.

Le possibilità che abbiamo individuato sono quindi soltanto cinque:

1. 1. 3 facce triangolari che si incontrano in ogni vertice: è il caso del tetraedro, che ha 4 facce triangolari e 4 vertici;
2. 2. 4 facce triangolari che si incontrano in ogni vertice: è il caso dell’ottaedro, che ha 8 facce triangolari e 6 vertici;
3. 3. 5 facce triangolari che si incontrano in ogni vertice: è il caso dell’icosaedro, che ha 20 facce e 12 vertici;
4. 4. 3 facce quadrate che si incontrano in ogni vertice: è il caso del cubo o esaedro, che ha 6 facce e 8 vertici;
5. 5. 3 facce pentagonali che si incontrano in ogni vertice: è il caso del dodecaedro, che ha 12 facce e 20 vertici.

Dadi e palloni

I solidi platonici forniscono lo spunto per comprendere e approfondire molti argomenti di interesse matematico, ma sono anche modelli straordinariamente utili per la realizzazione di oggetti per giocare: in particolare dadi e palloni.

Ciascuna di queste due tipologie di manufatto richiede attenzioni particolari nel processo di costruzione: a meno che non vogliamo fregare qualcuno, un dado deve innanzitutto essere equo, cioè tutte le sue facce devono avere la stessa probabilità di uscire durante un lancio, mentre un pallone deve essere il più possibile simile a una sfera.

Cominciamo dai dadi. I solidi platonici, evidentemente, grazie alla loro forma simmetrica, caratterizzata da facce regolari e uguali, e da vertici e spigoli equivalenti, costituiscono ottimi modelli di dadi equi.

Per gli appassionati di Dungeons and Dragons ciò non rappresenta una sorpresa: per questo gioco vengono infatti utilizzati dadi la cui forma riflette quella dei cinque dadi platonici.

Ma l’uso di dadi platonici non è certo un fatto recente. Negli anni Venti del secolo scorso, l’archeologo inglese Leonard Wooley fece un curioso ritrovamento all’interno delle tombe reali dell’antica città sumera di Ur: alcune tavole da gioco anticamente utilizzate per il cosiddetto Gioco Reale di Ur, l’antenato del moderno backgammon.

Come è visibile nella figura, la particolare scacchiera era formata da un rettangolo 8 × 3 privato di due caselle esterne su ciascuno dei lati lunghi. Ciascuno dei due giocatori utilizzava 7 pedine e 3 dadi a forma di tetraedro con le punte smussate. In ciascun dado, due dei quattro vertici erano marcati, affiché ogni lancio potesse produrre due possibili esiti, a seconda che il vertice rivolto verso l’alto fosse marcato o no. In pratica gettare un dado era come lanciare una moneta e vedere se è uscita testa oppure croce.

Il regolamento del gioco non è stato del tutto chiarito. Pare comunque che ogni giocatore dovesse partire da una delle caselle e arrivare a una casella terminale, determinando il numero di caselle percorse a ogni turno mediante il lancio dei dadi. La collisione con un pezzo avversario costringeva l’altro giocatore a ripartire dall’inizio. I simboli speciali disegnati su alcune caselle provocavano eventi particolari, come il pagamento o il ritiro di una posta.

Ma, oltre ai cinque platonici, ci sono altri solidi che possono essere sfruttati per costruire dadi equi? Ebbene sì: i matematici hanno scoperto che ne esistono in particolare altri venti, oltre a cinque famiglie formate ciascuna da un numero infinito di dadi equi.

E i palloni? Concentriamoci sui palloni da calcio (anche se si potrebbe scrivere forse un libro intero considerando la geometria di tutti i tipi di palle utilizzate nei vari sport).

Il problema della costruzione un pallone di cuoio per giocare a calcio è il seguente: non è possibile costruire una sfera perfetta (come invece si deve fare per le palline da ping pong), ma si deve cercare di approssimare una sfera cucendo insieme pezzi di cuoio. Inoltre, è comodo che i pezzi di cuoio siano tutti uguali, ed è ancora più comodo se questi pezzi vengono prodotti come poligoni regolari. Ecco quindi che i solidi platonici tornano utili anche in questo caso: preparando, per esempio, pezzi di cuoio a forma di triangolo equilatero si possono poi cucire tra di loro per realizzare una palla tetraedrica oppure ottaedrica oppure icosaedrica. Una volta il pallone viene gonfiato d’aria, le spigolosità si smussano, ottenendo qualcosa di vagamente simile a una sfera. È chiaro però che più sono le facce del solido più il pallone risulterà vicino a una forma sferica.

Ecco perché l’icosaedro è il modello platonico storicamente preferito dai costruttori di palloni da calcio. Ai mondiali messicani del 1970 l’Adidas presentò il suo mitico pallone Telstar, ottenuto da un icosaedro spianando i vertici: la forma risultante, il familiare pallone a esagoni bianchi e pentagoni neri, è ciò che i matematici chiamano icosaedro troncato, e che i chimici hanno ritrovato in una molecola di carbonio chiamata buckminsterfullerene, appartenente alla vasta famiglia dei fullereni. Il nome Telstar fu scelto per la somiglianza con l’omonimo satellite artificiale posto in orbita geocentrica e utilizzato nelle telecomunicazioni a partire dagli anni Sessanta.

Anche alcuni modelli più recenti di palloni da calcio si rifanno ai solidi platonici: il Brazuca dei Mondiali 2014 in Brasile è topologicamente un cubo, così come lo era il pallone dei primi Mondiali, quelli del 1930, mentre il Teamgeist, pallone ufficiale dei Mondiali tedeschi del 2006 vinti dall’Italia, era un ottaedro troncato.

I solidi platonici nell’arte

I solidi platonici sono sempre stati fonte di ispirazione per molti artisti. Piero della Francesca, che non fu soltanto un pittore, ma anche un matematico, era ossessionato dai solidi regolari: uno dei suoi trattati, il “De quinque corporibus regularibus”, era dedicato escludivamente a questi suggestivi poliedri, che all’artista interessavano ovviamente anche per il loro rapporto con il disegno e con le arti figurative.

Nell’articolo del numero 184 ricordavo come anche Leonardo Da Vinci realizzò moltissime illustrazioni inerenti ai solidi platonici, che furono pubblicate nel libro “De divina proportione” del frate matematico Luca Pacioli.

Nel 1955, il grande pittore surrealista Salvador Dalì realizzò una “Ultima cena” che stravolge i canoni dell’iconografia tradizionale. La scena è inserita all’interno di un grande dodecaedro, il solido regolare che Platone aveva associato alla perfezione dell’universo nel suo complesso. Nel descrivere il dipinto, Dalì parlò di una “cosmologia aritmetica e filosofica basata sulla sublime paranoia del numero dodici”. Sicuramente non è un caso che il numero delle facce del dodecaedro, 12, sia uguale al numero degli apostoli.

.

Un altro artista del Novecento che ha sfruttato a fini figurativi il fascino dei solidi platonici è stato l’olandese Maurits Cornelis Escher, autore di celebri costruzioni impossibili e di disegni geometrici di grande fascino. La sua famosa litografia “Cascata” mostra un piccolo villaggio caratterizzato da costruzioni paradossali, in cui dell’acqua sembra scorrere in salita. Sulla sommità delle due torri poggiano due grandi solidi, oggi noti come poliedri di Escher, la cui forma si può ottenere intrecciando tra di loro tre ottaedri.

La soluzione del problema

L’enigma di settembre descriveva un particolare dado tetraedrico, sulle cui facce sono indicati quattro numeri interi, che godono di alcune proprietà:

• • sono tutti diversi tra di loro;
• • sono tutti numeri primi;
• • uno dei quattro numeri ha una sola cifra;
• • ognuno degli altri tre numeri ha due cifre, la seconda delle quali è 3;
• • lanciando il dado, la somma dei numeri visibili dà sempre un numero primo.

I lettori erano invitati a determinare i numeri interi riportati sulle quattro facce del tetraedro.

La soluzione dell’enigma non era unica: anzi, ce n’erano ben cinque. Alcuni lettori sono stati bravi a indicarle tutte, anche se per considerare vinta la sfida era sufficiente individuarne una.

Le soluzioni erano le seguenti:

• • 5, 13, 23, 43
• • 5, 13, 43, 53
• • 5, 13, 43, 83
• • 7, 13, 23, 53
• • 7, 23, 73, 83

Non vi era un metodo particolare per individuare le soluzioni del problema: un approccio praticabile era quello per “forza bruta”, cioè per enumerazione e verifica delle possibili quaterne, da attuare a mano oppure con l’ausilio della potenza di calcolo di un computer (molti lettori, per esempio, si sono serviti di un foglio elettronico, strumento molto servizievole in casi come questo).

I vincitori

Il lettore che per primo ha inviato una risposta esatta è stato Mattia Caligiana, che si è aggiudicato l’abbonamento premio.

Gli altri lettori che hanno risolto correttamente l’enigma sono stati Davide Messina, Giorgia Hofer, Daniele Tosalli, Iacopo Longo, Alessio Aurigemma, Dario Broggi, Alberto Masini, Fabio Nevola, Michele D’Errico e Maurizio Carlino.

Complimenti al vincitore e a tutti i lettori che hanno saputo trovare la soluzione al problema!