La Coppa dei Mondi – approfondimenti sul quesito e soluzione

Il problema del calendario

Lo scorso 28 luglio è stato stabilito il calendario del campionato di calcio di Serie A 2014-15. Forse molti dei lettori si saranno a volte chiesti come si svolge tale procedura. Si tratta di una normale estrazione, come quando vengono sorteggiati i numeri del lotto, o di un complicato calcolo effettuato da un supercomputer?

Sicuramente definirlo sorteggio sarebbe riduttivo e semplicistico. Come spiegato nell’articolo di giugno, stabilire il calendario di un girone all’italiana, cioè di un torneo in cui ogni squadra disputa un incontro con ciascuna delle altre partecipanti, non è un’operazione banale, a meno che il numero delle formazioni non sia molto esiguo.

Come ho raccontato nel numero 182, Johann Berger, maestro di scacchi austriaco vissuto tra il 1845 e il 1933, inventò l’algoritmo più famoso tra quelli proposti per risolvere il problema. Purtroppo nella stampa della rivista è stato commesso un errore, per cui la descrizione di questo procedimento è risultata poco chiara. Coglierò l’occasione di queste note per togliere ogni dubbio sul funzionamento dell’algoritmo.

Nell’articolo si immaginava di dover stilare il calendario della Coppa dei Mondi 2514, le cui otto partecipanti sono Terra, Luna, Marte, Cerere, Ganimede, Europa, Callisto e Titano. La prima giornata è determinata semplicemente formando i quattro accoppiamenti che derivano dall’ordine in cui abbiamo elencato le squadre:

E la seconda giornata? Immaginiamo di mantenere la Terra fissa al suo posto in alto a sinistra, e facciamo ruotare in senso orario le altre squadre. Marte si ritroverà nella prima riga, a fianco della Terra. La Luna scenderà nella seconda riga, Cerere nella terza, ed Europa nella quarta. Titano passerà nella prima colonna, restando comunque nella quarta riga. Callisto salirà nella terza riga, spingendo Ganimede nella seconda. Il risultato sarà il seguente:

Proseguendo in questo modo si compileranno tutte le altre giornate del torneo, con la certezza che, alla fine, ogni squadra incontrerà ciascuna delle altre esattamente una volta.

Ma quante saranno le giornate? Se ogni squadra deve incontrare sette avversarie, è evidente che la Coppa si articolerà in sette giornate, in ognuna delle quali saranno disputate quattro partite. Il numero totale degli incontri sarà quindi 7 × 4 = 28.

In generale, se le squadre che partecipano a un girone all’italiana sono N (con N pari), le giornate saranno N-1, e, dato che ogni giornata comprenderà N/2 partite, saranno giocati in tutto N(N-1)/2 incontri. Tutto questo considerando il solo turno di andata: se è previsto anche il girone di ritorno le giornate saranno 2(N-1) e le partite N(N-1).

Nella Serie A del nostro campionato di calcio, che comprende N=20 squadre, vengono disputate 2(N-1) = 38 giornate, per un totale di N(N-1) = 380 partite.

E se le squadre fossero in numero dispari? In questo caso, a turno ognuna delle formazioni dovrebbe riposare, e il numero delle giornate uguaglierebbe così il numero delle partecipanti. In termini più formali, se le squadre sono N (con N dispari), le giornate saranno N. Visto che a ogni giornata si giocherebbero (N-1)/2 incontri, le partite complessive, prescindendo dal girone di ritorno, saranno N(N-1)/2: esattamente lo stesso risultato che avevamo ottenuto nel caso di N pari.

Per esempio, 19 squadre darebbero vita a un torneo di N = 19 giornate, per un totale di N(N-1)/2 = 171 gare.
Abbiamo così risposto al primo quesito proposto nel numero di giugno (peraltro abbastanza banale rispetto al secondo).

Altri algoritmi

Il metodo di Berger è l’unico possibile per risolvere il problema del campionato? No di certo. Esistono molti altri algoritmi adatti allo scopo. Sinceramente non so se nel sorteggio dei calendari dei campionati di calcio venga utilizzata una variante dell’algoritmo di Berger o un approccio computazionale completamente diverso.

Sicuramente il metodo “puro” di Berger non è utilizzabile in queste occasioni, perché nella determinazione delle giornate devono essere considerati molti vincoli supplementari. Per esempio si fa in modo che le partite tra le squadre più forti non vengano programmate nelle giornate iniziali del campionato, si evita che in una medesima giornata debbano giocare in casa squadre della stessa città, come Verona o Chievo, e così via.

È quindi ipotizzabile che il computer adibito alla determinazione dei calendari sia programmato con un algoritmo simile a quello proposto da Berger, ma modificato e perfezionato in modo da tener conto di una serie di constraint aggiuntivi.

Il problema del calendario del campionato mi ha affascinato fin da quando ero ragazzino. Quando avevo una dozzina d’anni, mi cimentavo, con un amichetto compagno di innumerevoli partite a pallone nei cortili di casa, nella compilazione dei calendari dei nostri campionati immaginari.

Ma gli algoritmi che adoperavamo erano molto rozzi e poco efficaci. Erano basati su un faticoso approccio per tentativi: si tentava di programmare giornata per giornata, e se a un certo punto incontravamo un ostacolo insormontabile (cioè scoprivamo che le ultime due squadre non ancora abbinate in una giornata si erano già incontrate in una giornata precedente), eravamo costretti a ricominciare tutto da capo.

Diversi anni dopo, non conoscendo ancora il metodo di Berger, escogitai un metodo molto più elegante per risolvere il problema in modo diretto. Supponiamo di avere N squadre. Costruiamo una tabella con N righe e N colonne: ogni riga e ogni colonna corrisponde a una delle squadre. Il nostro obiettivo è riempire ogni casella interna con un numero, che rappresenta la giornata in cui le due squadre in questione si incontreranno tra di loro.

Naturalmente, dobbiamo escludere le caselle della diagonale principale, corrispondenti alle improbabili partite in cui una squadra gioca contro se stessa. Per semplicità, possiamo anche trascurare metà tabella, per esempio quella sotto la diagonale principale, perché le caselle di questa zona rappresentano le stesse partite descritte nell’altra metà: potrebbero essere utilizzate per il girone di ritorno, ma una volta che è programmato il turno di andata, basta ripetere la sequenza delle partite, a campi invertiti, e anche il ritorno è determinato.

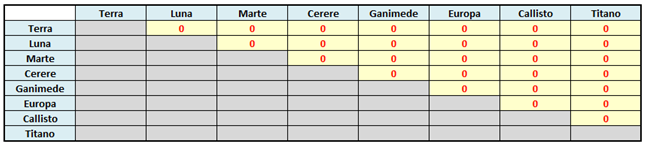
Considerando le N=8 partecipanti alla Coppa dei Mondi, la tabella di partenza sarebbe la seguente:

In generale, condizione necessaria e sufficiente affinché la compilazione di una simile tabella rappresenti un calendario valido per un campionato è che su ogni riga e su ogni colonna siano presenti tutti i numeri da 1 a N-1, senza ripetizioni.

Infatti, la ripetizione di un numero su una medesima riga o colonna starebbe a indicare che una squadra deve giocare due partite nella stessa giornata, e che, corrispondentemente, un’altra squadra non giocherebbe alcuna partita. Situazione questa ovviamente non accettabile.

Forse il vincolo della non ripetizione dei numeri su righe e colonne vi avrà fatto venire in mente il sudoku: in effetti una parentela c’è, ed esistono interessanti connessioni anche con altri concetti matematici come i quadrati latini e i problemi di colorazione dei grafi. Per i lettori interessati ai dettagli, rimando agli articoli del mio blog citati nella bibliografia.

Vediamo come si articola l’algoritmo. Si parte con la matrice compilata con degli zeri.

A questo punto ha inizio il ciclo principale. Si considera, una dopo l’altra, le squadre partecipanti, e per ciascuna vengono individuate la riga e la colonna corrispondenti. Immaginiamo di scendere dall’alto verso il basso lungo la colonna, “rimbalzare” sulla diagonale principale, e percorrere la riga verso destra. Lungo questo cammino, ogni volta che troviamo una casella ancora a zero, la riempiamo con un numero. Quale numero? Per ogni cammino, cercheremo la prima casella che possiamo riempire, e tenteremo di riempirla con il numero successivo a quello presente nella casella immediatamente precedente. Se si tratta della prima casella del cammino, tenteremo di piazzare un 1. Ad ogni nuovo tentativo di riempimento, cresceremo di 1.

Ogni volta che tentiamo di collocare un numero, comunque, controlleremo se il numero candidato non sia stato precedentemente collocato su un’altra casella dello stesso cammino, o della stessa riga, o della stessa colonna: in questo caso ritenteremo il riempimento con il numero aumentato di 1. Se, a un certo punto, a cammino non ancora completato, scopriremo di essere già arrivati a N-1 (nel nostro esempio 7), il successivo incremento ci farà ripartire da 1.

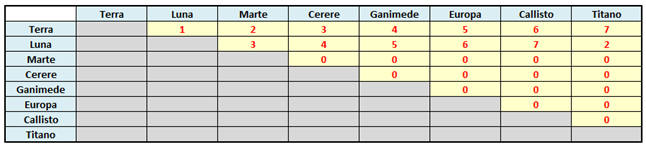
Percorrendo in questo modo il cammino relativo alla Terra, si ottiene:

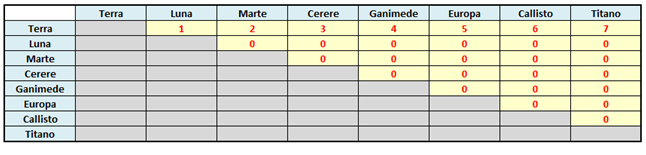Dopo aver “sistemato” anche la Luna, ci ritroveremo con questa tabella:

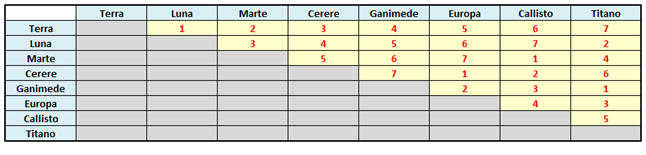
Alla fine dell’intero ciclo di “cammini”, la tabella si riempirà in questo modo:

A questo punto è facile “leggere” il calendario ottenuto. Per esempio, la prima giornata sarà composta dalle partite corrispondenti alle caselle riempite con un 1: Terra-Luna, Marte-Callisto, Europa-Cerere e Titano-Ganimede.

Come potete vedere, il risultato è diverso, già nella prima giornata, da quello prodotto dall’algoritmo di Berger. Questo non deve sorprendere, anzi. Con un numero di squadre appena un po’ grande, come 8, sarebbe infatti molto strano che due diversi approcci generassero calendari identici.

L’enigma

Il problema del numero di giugno consisteva nel pianificare il girone all’italiana della Coppa dei Mondi 2514 con le otto squadre già menzionate (Terra, Luna, Marte, Cerere, Ganimede, Europa, Callisto e Titano), facendo però in modo di rispettare lo strano vincolo imposto dagli immaginari organizzatori: a ogni giornata due partite sono in programma al pomeriggio e due alla sera, e prese due squadre qualsiasi tra le partecipanti, esse giocheranno alla stessa ora soltanto tre volte (compresa la giornata in cui si troveranno a gareggiare l’una contro l’altra), mentre nelle altre occasioni scenderanno in campo in fasce orarie diverse.

Ad aggiudicarsi l’abbonamento semestrale è stata, questa volta, la lettrice Alessandra Guido, che ha proposto il seguente calendario:

Come potete constatare, la programmazione della nostra lettrice rispetta in pieno il vincolo imposto. Se prendiamo, per esempio, Terra e Luna, è facile notare che queste due squadre giocheranno alla stessa ora alla prima giornata (quando giocheranno l’una contro l’altra), alla seconda (quando entrambe scenderanno in campo di pomeriggio), e alla terza (quando giocheranno entrambe in notturna), mentre in tutte le altre giornate si troveranno a disputare i loro incontri in orari differenti.

Anche Vito Squicciarini ci ha inviato, primo fra tutti, un calendario corretto: ma avendo già vinto l’abbonamento lo scorso mese, il premio va alla seconda arrivata.

Il problema non era affatto di facile risoluzione: congratulazioni vivissime, quindi, ai due bravissimi risolutori. Al prossimo enigma!

Link per approfondire

Ecco un “trittico” di post dedicati all’argomento, con alcuni dettagli matematici per i lettori più curiosi:

http://misterpalomar.blogspot.it/2011/01/il-problema-del-campionato-parte-1.html

http://misterpalomar.blogspot.it/2011/01/il-problema-del-campionato-parte-2.html

http://misterpalomar.blogspot.it/2011/01/il-problema-del-campionato-parte-3-con.html