Il quesito posto nella “puntata” di luglio-agosto della nuova rubrica Moebius riguardava il legame tra due famosi rompicapi matematici: le torri di Hanoi, inventate da Édouard Lucas nel 1883, e il gioco icosiano ideato da Sir William Rowan Hamilton nel 1857.
Lucas fu un grande matematico, noto per alcuni studi sui numeri primi e sui numeri di Fibonacci, ma fu anche un importante divulgatore e creatore di giochi. Per promuovere efficacemente il rompicapo della torre di Hanoi, non solo si inventò la leggenda dei monaci raccontata nell’articolo, ma utilizzò un ingegnoso pseudonimo: “N. Claus (de Siam)”, anagramma di “Lucas D’Amiens” (Amiens era la sua città natale). Le cronache raccontano che morì di setticemia a soli 49 anni, a causa di una ferita provocata dalla caduta di un piatto rotto sulla sua guancia, durante un pranzo di gala.
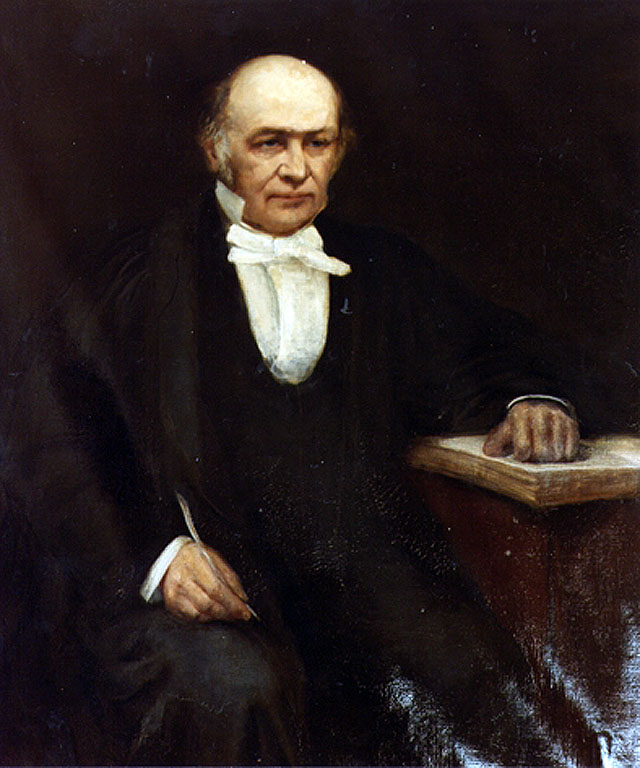
Il dublinese Hamilton, invece, è famoso per le sue ricerche a cavallo tra fisica e matematica: i suoi contributi in questo campo si sono rivelati fondamentali per il successivo sviluppo della meccanica quantistica. Pare che parlasse correntemente una quindicina di lingue, e che avesse conosciuto personalmente il poeta romantico William Wordsworth.
Il culmine della sua carriera coincise con la sua nomina a professore di astronomia al Trinity College di Dublino e ad Astronomo Reale d’Irlanda.
Le regole dei due giochi sono descritti nell’articolo “C’è ancora tempo”, pubblicato su Coelum 172. Se desiderate qualche approfondimento, potete consultare i libri e link che trovate in fondo.
Il rompicapo di Lucas ha sicuramente riscosso maggiore fortuna rispetto a quello di Hamilton, forse grazie alla sua maggiore “giocabilità”: su internet troverete un sacco di siti che parlano delle torri di Hanoi, ma pochi che descrivono il gioco icosiano.
È anche facile trovare versioni commerciali del gioco di Lucas nei negozi specializzati (io stesso ne ho una, e la utilizzo durante i miei laboratori didattici). Qualche tempo fa, trovai una versione gigante delle torri di Hanoi nel parco della Venaria Reale a Torino. Se passate di là, adesso che sapete come si risolve questo celebre enigma, non dimenticate di mostrare la vostra capacità davanti agli altri turisti: farete un figurone!
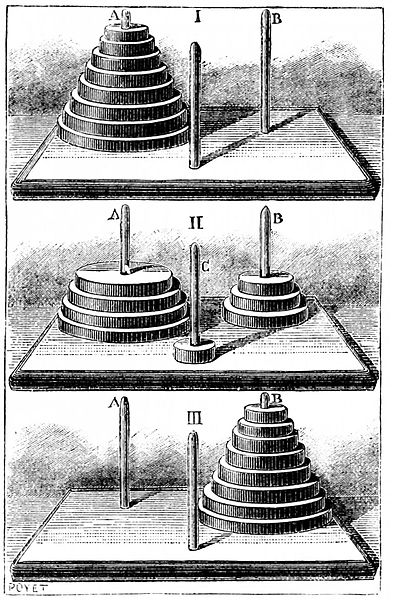Al contrario, che io sappia, il rompicapo di Hamilton non è più sul mercato da molti decenni: nella fotografia qui a destra potete vedere il contenuto della ottocentesca versione commercializzata dallo stesso Hamilton.
Entrambi i rompicapi, comunque, sono di notevole interesse matematico: non soltanto il gioco dei monaci vietnamiti, il cui metodo risolutivo è un esempio classico di algoritmo ricorsivo, ma anche il gioco di Hamilton, che ha dato il nome ai percorsi hamiltoniani, fondamentali nella teoria dei grafi.
Indice dei contenuti
Ma veniamo alla soluzione del quesito di luglio-agosto.
Innanzitutto consideriamo il gioco delle torri di Hanoi con tre dischi, e chiamiamo questi ultimi X, Y e Z, in ordine di dimensione crescente.
Se disponiamo i tre dischi nell’ordine in cui devono essere spostati per risolvere il rompicapo, otteniamo la sequenza XYXZXYX. Interpretando i tre simboli X, Y, Z come le tre dimensioni spaziali di un cubo, ad esempio lunghezza, larghezza e altezza, la sequenza ottenuta ci guiderà sugli spigoli del cubo per percorrere un circuito hamiltoniano. Ecco trovato il nesso nascosto tra questi due giochi, apparentemente lontani l’uno dall’altro.
E se i dischi fossero più di tre? Nessun problema: l’analogia sussiste ancora, a condizione che ricorriamo a ipercubi con più di tre dimensioni.
Il primo a suggerire questo legame tra i due rompicapi fu Martin Gardner, uno dei giganti della matematica ricreativa, nel suo articolo riportato nella seguente bibliografia.
Riferimenti bibliografici
- Edouard Lucas, Récréations mathematiques, III, Albert Blanchard, 1979.
- Martin Gardner, Il gioco dell’icosaedro e la torre di Hanoi, in Enigmi e giochi matematici, Milano, Rizzoli, 2001.
- Fred Schuh, The master book of mathematical recreations, Dover, 1968.
Link
- Dal mio blog “Mr. Palomar”, un post sul gioco della torre di Hanoi.
- Sulla torre di Hanoi:
http://areeweb.polito.it/didattica/polymath/htmlS/probegio/GAMEMATH/Hanoi/Hanoi.htm
http://cut-the-knot.com/recurrence/hanoi.html
http://mazeworks.com/hanoi/index.htm
- Sul gioco icosiano: http://puzzlemuseum.com/month/picm02/200207icosian.htm
