Home Articoli e Risorse On-Line Quiz di Logica Matematica e Astronomia Palomar Cube – approfondimenti sul quesito e soluzione

Palomar Cube – approfondimenti sul quesito e soluzione

10 Febbraio 2014

12 views

Indice dei contenuti

La soluzione

Va detto subito: non era per niente facile. Per questo il mio plauso più sincero va subito ai tre lettori che si sono cimentati nel problema e hanno inviato la soluzione corretta in redazione.

In ordine di tempo i risolutori sono stati: Daniele Tosalli, Maurizio Carlino e Michele D’Errico.

Il primo ha inviato una soluzione in cui la somma costante è uguale a 12. Ha escogitato una rappresentazione molto ingegnosa del cubo, allo scopo di raffigurare tutti i numeri associati ai 54 quadratini.

Ecco la sua soluzione, che gli è valsa l’abbonamento semestrale alla rivista:

Tosalli ha ammesso che il cubo di Rubik è il suo gioco preferito, e ha raccontato di essere partito col piede sbagliato, pensando che la somma dovesse essere 10. Poi ha capito che 12 poteva essere un numero più promettente. Infatti i cubetti d’angolo sono 8, e quelli e di metà spigolo sono 12: quindi sono in tutto 20, e 20 x 12 = 240; ora, dato che su ognuna delle 6 facce ci sono tutti i numeri da 1 a 9, la somma complessiva dei numeri è pari a (1+2+3+…+9)x6 = 270. Quei 30 mancanti, ha pensato Tosalli, si suddivideranno tra i 6 quadratini posti al centro delle facce.

Il nostro lettore ha addirittura modificato uno dei suoi cubi di Rubik, sostituendo i bollini colorati con adesivi bianchi e numerandoli poi con un pennarello secondo lo schema trovato. Quindi si è cimentato in un rompicapo del tutto inedito: mescolare il nuovo cubo “pseudo-Rubik”, con i numeri da 1 a 9 al posto dei sei colori, e tentare di riordinarlo!

E’ davvero meraviglioso constatare come questo brillante lettore di Coelum abbia preso ispirazione dall’enigma originario da me proposto per inventarne un altro, forse ancora più interessante.

Se Tosalli ha risolto l’enigma per primo e si è inventato un nuovo rompicapo, un altro lettore, Maurizio Carlino, ha inviato in redazione un’analisi del problema splendidamente rigorosa ed esaustiva. Abbiamo ritenuto giusto riportarla integralmente, anche perché in essa Carlino dimostra in modo ineccepibile come le soluzioni posssibili dell’enigma siano associate alle somme 11, 12 e 13 (quindi non soltanto 12).

Non avrei potuto fare di meglio di questo lettore per offrire una panoramica completa e “definitiva” sul problema. La lettura non è semplice, ma i lettori esigenti e appassionati di matematica la troveranno molto utile.

Nel contesto di questa trattazione così impeccabile, mi è piaciuta particolarmente l’idea di introdurre la definizione formale di “Palomar Cube”: chissà che un giorno qualche paper scientifico non riprenda questa terminologia, assicurandola definitivamente al lessico matematico (sto scherzando, ma non si sa mai).

Ed ecco a voi l’esposizione di Carlino, tra l’altro corredata di magnifiche immagini, al quale vanno i miei più sentiti complimenti:

L’angolo delle notazioni

Indichiamo con:

#ca = numero di cubetti ad angolo, ossia 8
#cms = numero di cubetti di metà spigolo, ossia 12
Σ(ca) la somma dei 3 valori che appaiono su un cubetto ad angolo
Σ(cms) la somma dei 2 valori che appaiono su un cubetto di metà spigolo
n(d,i,j) il numero che compare sulla d-faccia del Palomar Cube in posizione (i,j):
n(d,i,j) = {1,..,9} per ogni 1≤ d ≤ 6

Assumiamo che le facce siano numerate come quelle di un dado e che le posizioni su ciascuna faccia siano numerate come in una matrice 3×3. Poiché le facce sono numerate come quelle di un comune dado, le facce 1-6, 2-5 e 3-4 sono opposte tra loro. Se d e d* sono due facce opposte del PC definiamo coniugato dell’elemento (d,i,j) l’elemento che corrisponde a (d*,i*,j) dove i*=(10-i)mod6.

Ad esempio il coniugato di (1,1,1) è (6,3,1), mentre il coniugato di (2,2,3) è (5,2,3).

Con questa notazione il numero associato al cubetto centrale sulla d-faccia di un PC è n(d,2,2) (che ha come coniugato (d*,2,2)) ed inoltre Σ(cc) = Σ(n(d,2,2)) rappresenta la somma dei valori attribuiti a tutti i cubetti centrali del PC.

Che cos’è un “Palomar Cube”

Un “Palomar Cube” è per definizione un cubo numerico con la seguente proprietà:

per ogni ca e per ogni cms: Σ(ca) = Σ(cms) = k

k può valere solo 11,12 o 13

Dimostriamo innanzitutto che k è tale che:
10 < k < 14, ossia k può valere11,12, o 13 ऀ(R1)

Osserviamo che per ogni d-faccia:
Σ(n(d,i,j)) = (9*10)/2 = 45

e quindi su tutto il PC:
Σ(n(d,i,j)) = 270

Poiché Σ(ca)= Σ(cms)=k e poiché #ca=8 e #cms=12 allora deve essere:
20k+ Σ(cc) = 270 ऀऀऀ(R2) e quindi k < 14.

Inoltre se ponessimo per ipotesi k ≤ 10 allora 20k ≤ 200 ma poiché Σ(cc) ≤ 54 allora la (R2) risulterebbe non vera. Di conseguenza k > 10.

Caratteristica di simmetria

In base alla notazione prescelta, la condizione Σ(ca) = k può essere espressa per ogni cubetto d’angolo in funzione dei numeri che compaiono su ciascuna delle 3 facce come segue:

n(1,1,1)+n(2,1,1)+n(4,1,3) = k
n(1,1,3)+n(4,1,1)+n(5,1,3) = k
n(1,3,1)+n(2,1,3)+n(3,1,1) = k
n(1,3,3)+n(3,1,3)+n(5,1,1) = k
n(6,3,1)+n(5,3,1)+n(3,3,3) = k
n(6,3,3)+n(3,3,1)+n(2,3,3) = k
n(6,1,1)+n(5,3,3)+n(4,3,1) = k
n(6,1,3)+n(4,3,3)+n(2,3,1) = k

dove le 5a-8a sono le relazioni valide per i valori coniugati – termine per termine – delle 1a-4a.

Analogamente la condizione Σ(cms) = k può essere espressa per ogni cella di metà spigolo come:

n(1,1,2)+n(4,1,2) = k
n(1,2,1)+n(2,1,2) = k
n(1,3,2)+n(3,1,2) = k
n(1,2,3)+n(5,1,2) = k
n(2,2,1)+n(4,2,3) = k
n(2,2,3)+n(3,2,1) = k
n(6,3,2)+n(3,3,2) = k
n(6,2,3)+n(2,3,2) = k
n(6,1,2)+n(4,3,2) = k
n(6,2,1)+n(5,3,2) = k
n(5,2,1)+n(3,2,3) = k
n(5,2,3)+n(4,2,1) = k

dove anche qui le 7b-12b sono le relazioni valide per i valori coniugati – termine per termine – delle 1b-6b.

Naturalmente risulterà anche:

n(1,2,2)+n(2,2,2)+n(3,2,2)+n(4,2,2)+n(5,2,2)+n(6,2,2) = Σ(cc) = 270 – 20k

Per i nostri scopi possiamo allora senz’altro assumere nel seguito che n(d,i,j) = n(d*,i*,j).

In questo modo, sarà altresì possibile determinare univocamente i valori dell’intero cubo attraverso tutti i valori attribuiti a 3 facce.

Soluzione per k=13

Si nota immediatamente che ‘1’,‘2’ e ‘3’ non possono essere assegnati come valori delle celle di metà spigolo, poiché non esiste alcun valore che possa soddisfare le 1b-12b. Di conseguenza questi valori possono essere attribuiti solo ai cubetti d’angolo o ai cubetti centrali.

Dalla 1c deriva inoltre che Σ(cc) = 10 per cui è necessario scegliere per i cubetti centrali 6 valori la cui somma è 10. Possiamo considerare valida per i nostri scopi la sequenza (1,1,3,1,1,3).

Ne deriva che i restanti due ‘1’, i sei ‘2’ e gli altri quattro ‘3’ sono necessariamente valori da assegnare ai cubetti d’angolo. Una possibile assegnazione è quella in cui i due ‘1’ e i sei ‘2’ sono attribuiti a cubetti diversi, mentre i quattro ‘3’ sono distribuiti equamente tra gli ‘1’ e i ‘2’. Ne risulta la seguente sequenza (ogni riga rappresenta un elemento delle 8 terne):
(x x y y n n k k)
(3 3 3 3 t t r r)
(1 1 2 2 2 2 2 2)

Si vede allora subito che le due x sono determinate univocamente dal valore ‘9’, mentre le due y dal valore ‘8’. Ne deriva anche che nei valori dei cubetti d’angolo sono necessariamente da annoverare anche due ‘4’ e due ‘5’ che senza i due ‘9’ e i due ‘8’ non possono reciprocamente “accoppiarsi” nelle celle di metà spigolo. La nuova configurazione diventa quindi:
(9 9 8 8 n n k k)
(3 3 3 3 4 4 5 5)
(1 1 2 2 2 2 2 2)

che viene immediatamente “soddisfatta” attribuendo alle incognite i valori 7 e 6, ossia
(9 9 8 8 7 7 6 6)
(3 3 3 3 4 4 5 5)
(1 1 2 2 2 2 2 2)

Abbiamo trovato in questo modo 8 terne da associare agli 8 cubetti ad angolo; i valori per i dodici cubetti di metà spigolo saranno di conseguenza rappresentati dalle 3 coppie residue (9,4), (8,5) e (7,6) ciascuna presente 4 volte, ossia:
(9 9 9 9 8 8 8 8 7 7 7 7)
(4 4 4 4 5 5 5 5 6 6 6 6)

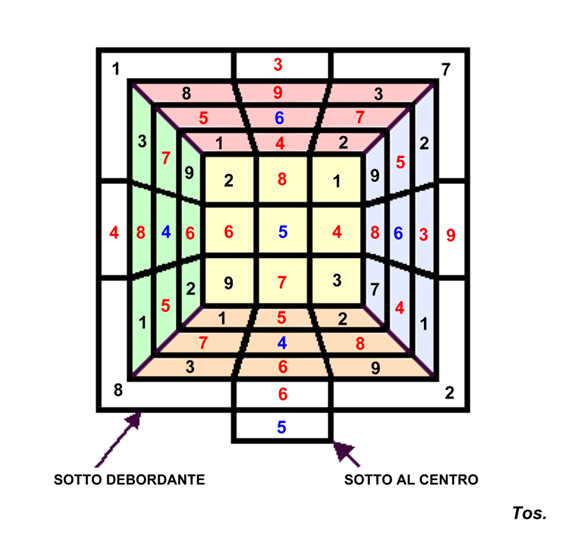
Si noti che sia le terne che le coppie sono uguali a due a due: in questo modo è possibile assegnarli come valori di elementi coniugati del “Palomar Cube”, ad esempio secondo lo schema nell’immagine qui a destra.

Soluzione per k=12

Si nota immediatamente che ‘1’ e ‘2’ non possono essere assegnati come valori delle celle di metà spigolo, poiché non esiste alcun valore che possa soddisfare le 1b-12b. Di conseguenza questi valori possono essere attribuiti solo ai cubetti d’angolo o ai cubetti centrali.

Dalla 1c deriva inoltre che: Σ(cc) = 30 per cui è necessario scegliere per i cubetti centrali 6 valori la cui somma è 30. Possiamo considerare valida per i nostri scopi la sequenza (5,7,3,5,7,3).

Ne deriva che i sei ‘1’, i sei ‘2’ ed almeno due ‘9’ sono necessariamente valori da assegnare ai cubetti d’angolo. Una possibile assegnazione è quella in cui i sei ‘1’ e i due ‘2’ sono attribuiti a cubetti diversi, mentre i quattro ‘2’ restanti saranno distribuiti equamente tra gli ‘1’ e i ‘2’. Ne risulta la seguente sequenza (ogni riga rappresenta un elemento delle 8 terne):
(9 9 y y n n k k)
(2 2 2 2 x x r r)
(1 1 2 2 1 1 1 1)

Si vede allora subito che le due y sono determinate univocamente attribuendo il valore ‘8’; ne deriva anche che nei valori dei cubetti d’angolo sono necessariamente da annoverare anche due ‘4’ che senza i due ‘8’ non possono reciprocamente “accoppiarsi” nelle celle di metà spigolo. La nuova configurazione diventa quindi:
(9 9 8 8 n n k k)
(2 2 2 2 4 4 r r)
(1 1 2 2 1 1 1 1)

che può essere soddisfatta” attribuendo a n il ‘7’ a k il ‘6’ ed a r il ‘5’, ossia
(9 9 8 8 7 7 6 6)
(2 2 2 2 4 4 5 5)
(1 1 2 2 1 1 1 1)

I valori per i dodici cubetti di metà spigolo saranno quindi rappresentati dalle 2 coppie residue (6,6) e (7,5) e dalle 4 coppie (8,4) e (9,3) ossia:
(9 9 9 9 8 8 8 8 7 7 6 6)
(3 3 3 3 4 4 4 4 5 5 6 6)

Si noti che sia le terne che le coppie sono uguali a due a due: in questo modo è possibile assegnarli come valori di elementi coniugati del “Palomar Cube”, ad esempio secondo il seguente schema.

Soluzione per k=11

Si nota immediatamente che ’1’ non può essere assegnato come valore delle celle di metà spigolo, poiché non esiste alcun valore che possa soddisfare le 1b-12b. Dalla 1c deriva inoltre che Σ (cc) = 50, per cui ‘1’ non può essere assegnato a nessun cubetto centrale, ma solo ai cubetti d’angolo.

Poiché Σ (cc) = 50 possiamo considerare valida per i nostri scopi la sequenza: (9,9,7,9,9,7).

Ne deriva che almeno quattro ‘2’ e due ‘4’ sono necessariamente valori da assegnare ai cubetti d’angolo. Una possibile assegnazione è la seguente:
(x x y y n n k k)
(1 1 2 2 p p q q)
(1 1 1 1 2 2 4 4)

Si vede allora subito che le due x e le due y sono determinate univocamente attribuendo loro rispettivamente il ‘9’ e l’8’; ne deriva anche che nei valori dei cubetti d’angolo sono necessariamente da annoverare anche altri due ‘2’ e due ‘3’ che senza i due ‘9’ e i due ‘8’ non possono“accoppiarsi” nelle celle di metà spigolo. La nuova configurazione diventa quindi:
(9 9 8 8 n n k k)
(1 1 2 2 2 2 3 3)
(1 1 1 1 2 2 4 4)

che viene immediatamente “soddisfatta” attribuendo i valori 7 e 4, ossia
(9 9 8 8 7 7 4 4)
(1 1 2 2 2 2 3 3)
(1 1 1 1 2 2 4 4)

I valori per i dodici cubetti di metà spigolo saranno rappresentati dalle 6 coppie residue (6,5) dalle 4 coppie (8,3) e dalle due coppie (7,4) ossia:
(8 8 8 8 7 7 6 6 6 6 6 6)
(3 3 3 3 4 4 5 5 5 5 5 5)

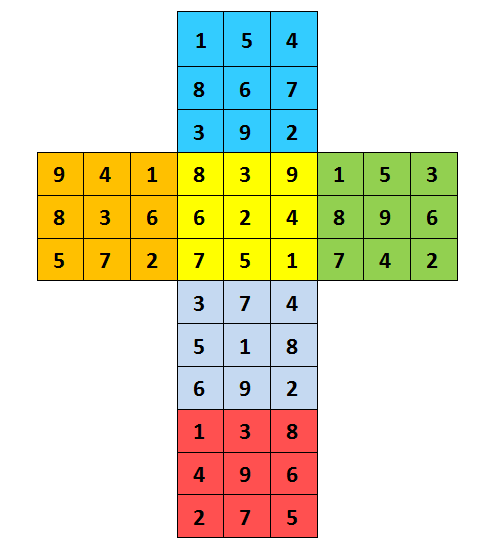Il terzo lettore che ha inviato una soluzione dell’enigma è stato Michele D’Errico, che ha optato per una delle soluzioni con somma uguale a 12. Riportiamo qui la figura inviata dal lettore.