Era proprio un momento critico, per Kirk. Non deve essere piacevole avere un flotta Klingon appostata come un gatto – e presumibilmente molto più veloce di ogni possibile gatto – pronta a farti a pezzettini. L’unica possibile consolazione, per il nostro, è che ci sono stati diversi lettori che, se non sono riusciti pienamente a toglierlo dalla brace, quanto meno ci hanno provato.
Cominciamo però con una nota a margine: la disquisizione sul limite di velocità all’interno dei sistemi planetari ha suscitato l’osservazione di Lorenzo Brandi, che ci ha ricordato che, ipotesi fantascientifiche a parte, il limite di velocità esiste davvero, nell’universo, e non solo all’interno dei sistemi solari. Per mostrarcelo, ci ha inviato la figura qua a fianco, che non si può negare che sia esplicativa.
Per quanto riguarda invece i suggerimenti strategici destinati al comandante dell’Enterprise, ne abbiamo alcuni che si limitano a descrivere i movimenti da attuare, altri che si avventurano in qualche calcolo geometrico. In ogni caso, assai spesso il tema che fa da sottofondo è sempre l’osservazione basilare che, per scappare via, Kirk deve percorrere un raggio di sfera, mentre i Klingon devono percorrere una semicirconferenza. Da qui si ricaverebbe facilmente il rapporto massimo consentito tra le due velocità (Klingon/Enterprise), che sarà strettamente apparentato con pi greco.
In questo senso, tutto sommato, si muove la proposta di Alfredo Paturzo, che ci scrive:
- L’unica strategia logica che mi viene in mente è che il capitano Kirk deve attirare a un estremo limite del confine (in un punto qualsiasi) l’astronave Klingon, dopodiché invertirà improvvisamente la rotta per precipitarsi alla massima velocità nel punto opposto, passante dal centro del sistema, della circonferenza che ipoteticamente lo delimita. Ora, se la velocità (o il tempo, fa lo stesso) dell’Enterprise è, poniamo, uguale a 1, e quella dei nemici non è superiore a c/2, cioè 1,57 volte questo valore, corrispondente alla semicirconferenza del cerchio che delimita il sistema solare, per Kirk e truppa è cosa fatta!
La novità introdotta da Alfredo consiste, insomma, nel tentare di costringere i Klingon a percorrere una intera semicirconferenza (invece che un quarto) mentre Kirk percorre un diametro (anziché un raggio). In breve, raddoppia il percorso per amplificare le differenze dei percorsi sub-luce. Non è in fondo troppo diverso da quanto suggerisce Maurizio Leotta che si lancia in qualche calcolo:
Astronavi: B = Capitano Kirk (Buoni); C = Klingon (Cattivi).
Le due astronavi sono considerate puntiformi.Il raggio di azione delle armi di C è trascurabile rispetto alle distanze in gioco. Sfera S: contiene il Sistema Planetario, ha raggio pari a r.
Astronave B: all’interno di S viaggia a velocità V, all’esterno di S viaggia a velocità infinita.
Astronave C: non può accedere all’interno di S. All’esterno di S viaggia a velocità K > V
Soluzione:
B si posiziona al centro di S. C, cercando di minimizzare la distanza che la separa da B è sempre in un punto tangente a S. Esiste, unica, una retta f passante per B e C (e per il centro di S che coincide con B). Questa retta interseca la sfera nei punti p1 (che coincide con C) e p2.
La navicella B imposta una rotta lungo f in direzione p2 cioè opposta a quella in cui si trova C. B deve percorrere uno spazio pari a r per raggiungere p2 cioè il bordo esterno della sfera. Quindi la rotta di B è lunga r. C non può entrare nella sfera e imposta la rotta più breve in direzione del punto p2 in cui B uscirà dalla sfera. La rotta di C è una semicirconferenza di raggio r giacente sulla sfera S e ha come partenza p1 e arrivo p2 (C ne sceglie una tra le infinite possibili).
La rotta di C è lunga pr.
Conclusione: Se (C viaggia a velocità K < pV ), allora l’astronave B riesce a sfuggire. Altrimenti l’astronave B viene distrutta.
Un po’ più complessa è la visione di Andrea Mattei, che impone qualche vincolo in più (ad esempio, il “centro” del sistema solare dovrebbe ospitare il Sole, quindi non è probabilmente divertente metterlo in traiettoria) e che infatti scrive:
La strategia da attuare, affinché la navicella Enterprise sfugga ai Klingon è la seguente: supponiamo che il cerchio che definisce il sistema solare sia la massima distanza del “pianeta” Plutone, quindi abbiamo definito le nuove Colonne d’Ercole. Come detto nel quesito, l’astronave dei Klingon è più veloce (almeno finché l’Enterprise è all’interno del Sistema Solare), quindi supponendo che l’Enterprise si avvicini ai confini rimanendo a una distanza “epsilon” del confine che rappresenta la distanza di sicurezza per non essere colpita, come supposto, l’astronave aliena si porterà immediatamente nei pressi dell’Enterprise. A questo punto l’Enterprise inverte la rotta tagliando il cerchio del Sistema Solare lunga la CORDA AB (dico la CORDA e non il diametro supponendo che l’astronave deve mantenersi ad una certa distanza dal Sole, che rappresenta il centro del cerchio, per cui non può attraversare il centro). L’astronave aliena deve invece percorrere l’arco di circonferenza per arrivare dal punto A al punto B+Epsilon che ovviamente è un tragitto superiore! Se come detto, la velocità dell’astronave Klingon non è di molto superiore a quelle dell’Enterprise non riuscirà a percorrere in tempo l’arco di circonferenza e quindi l’Enterprise uscita dal Sistema Solare potrà “filarsela” in tutta tranquillità! Traducendo in numeri la strategia esposta, si potrebbe calcolare qual è la velocità dell’astronave Klingon entro la quale non potrà raggiungere l’Enterprise.
Raggio del sistema Solare pari all’AFELIO di Plutone: r=7.375.000.000km.
Distanza minima dal Sole, per convenzione adottiamo il Perielio di Mercurio: d=46.000.000 km
Epsilon=distanza di sicurezza per non essere colpiti, la consideriamo trascurabile ai fini del calcolo.
L’angolo Alfa che determina l’arco da percorrere è l’arco-cotangente(r/d), ma approssimiamo a 180°. Quindi l’Arco di circonferenza che deve compiere l’astronave Klingon è:
Arco=2*Pi*r*Alfa/360 = con buona approssimazione alla semicirconferenza del nostro cerchio
quindi:
Arco=(2 * 3.1415926 * 7375000000 * 180) / 360 = 23.169.245.820 km
Per la stessa approssimazione stabiliamo che il percorso dell’Enterprise è pari al diametro del cerchio:
AB= 2 * 7.375.000.000 = 14.750.000.000 km
Quindi l’astronave Klingon deve percorrere 23,16 miliardi di km mentre l’Enterprise “solo” 14,75
Il rapporto 23,16 / 14,75 = 1.57 indica che, se l’astronave Klingon ha una velocità pari a 1,57 volte a quella dell’Enterprise, allora raggiungerà la nostra astronave nel momento in cui essa fuoriesce dal Sistema Solare
Il fatto significativo è che tutte le soluzioni fin qui esposte hanno una certa logica “statica”, mentre i generali – specialmente quelli che guidano astronavi – di solito hanno una visione decisamente dinamica. La domanda da porsi, infatti, è questa: ammettiamo pure che inizialmente la strategia delle due navi sia quella descritta, ovvero, riducendo il tutto a due dimensioni e, per ulteriore semplificazione, descrivendo il cerchi del sistema solare come fosse il quadrante d’un orologio, che entrambi le navi siano in corrispondenza delle ore 12, quando ad un tratto Kirk si dirige a tutta birra verso il diametralmente opposto “ore 6”.
Supponiamo che Klingon percorra la semicirconferenza che passa da ore 11, 10, etc., e ipotizziamo pure il caso delle velocità limite, ovvero che Kirk percorra il suo diametro nello stesso tempo esatto in cui i Klingon percorrono la loro semicirconferenza. Ebbene, consideriamo un attimo come si trovano le due navi a metà strada: l’Enterprise è esattamente al centro del quadrante (a cuocere sul sole, come nota giustamente Andrea), e i Klingon sono esattamente ad “ore 9”. Ora, secondo voi, Kirk è totalmente scemo e continua imperterrito a dirigersi verso ore 6, o giunti al centro farà piuttosto una brillante virata dirigendosi dritto verso “ore 3”, che in quel momento è decisamente più scomodo per i Klingon da raggiungere?
In altri termini, il problema è dinamico, e per le velocità finora considerate, Kirk non avrebbe problemi a scappare. Ma il bello è che Kirk riesce a scappare anche se i Klingon hanno velocità ben maggiori. La strategia, però, si basa su continui cambiamenti di rotta, come ha ben intuito il vincitore di questo mese, Pierangelo Bellini. Il quale, tra l’altro, si è dimostrato anche valentissimo disegnatore:
In realtà la Enterprise può usare 2 soluzioni:Soluzione UNO : – ) “Quasi sempre in poppa”.
Soluzione DUE : – ) “Vai per 45 gradi”.
Premetto che :
– Suppongo un sistema planetario del diametro 2r =100 U.A.;
– Una decina di UA sono sufficienti per riparare la E. dalle armi dei K.;
– La velocità minima dei K. necessaria e sufficiente per il gioco, quella che userò io, è PIGRECO volte quella della velocità della Enterprise; (cfr. Fig.0) cioè tale che se la Enterprise fugge diametralmente sul raggio EZ, la nave Klingon la raggiunge percorrendo la semicirconferenza KZ, proprio nel punto Z (talora A sui disegni) e addio Kirk. Per velocità inferiori della K., non esiste lotta perchè E. fugge come vuole;
– ho trasformato le “mosse” = “vettori distanza percorsa” da infinitesime a finite; ho il terribile sospetto che non sia corretto ma … tant è …
– ho indicato le “mossè” usando la stessa, una sola, successione numerica per le 2 astronavi.
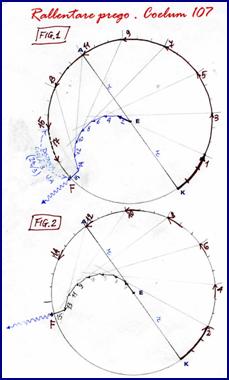Soluzione UNOKirk sceglie la tattica di New Zealand vs Luna Rossa, tenendo sempre la E. fra i K. ed il punto di fuga F (variabile), sulla stessa linea; solo in vicinanza (distanza minore di 1 “mossa”) del confine del sistema planetario, fa scattare la Enterprise perpendicolarmente alla circonferenza.
Quando la “mossa” successiva sta ai K., già la Enterprise è in fuga iperspaziale o roba così. Il giochetto di Kirk funziona sia che la prima mossa la faccia E sia che la faccia K (cfr Fig.1 e 2). Ho considerato anche il caso di una inversione di rotta della K. (Fig.3) che però da, così facendo, un vantaggio di 2 mosse alla E. (ciò ad ogni inversione, se eventualmente ripetuta ….).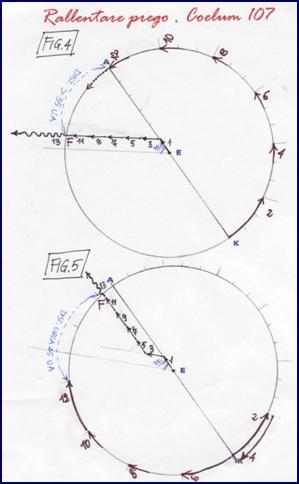
Soluzione DUENon soddisfatto dell’irregolarità finale della traiettoria della E., il capitano Kirk suggerisce un altro “scenario” per la fuga, in cui il punto di fuga F giace nel settore circolare, di angolo al centro di 45 gradi, “opposto” all’arco di traiettoria dell’inseguitore K (cfr. Fig. 4 e 5); la traiettoria di E. è una “spezzata” dai lati con direzione e verso del raggio EA o del raggio che forma 45 gradi con esso. Anche così, le inversioni di rotta dei K. non danno risultati a loro favorevoli.
La direzione “a 45 gradi”, discorde col moto dei K., viene scelta per allontanarsi dai punti di certa distruzione, quali il punto A diametralmente opposto ai K e il punto segnato dal raggio ortogonale a questo diametro.
Questa tattica di difesa ha il pregio di una maggiore semplicità descrittiva e non ha eccezioni ineleganti.
Entrambe le soluzioni danno alla Enterprise decine di UA di vantaggio, almeno con “mosse” non infinitesime!
Mi dispiace di non essere in grado di rappresentare in termini astratti, analitico-matematici, queste situazioni ma trovo consolazione nelle parole di S.Hawking che ammetteva di trovare difficoltà nel rappresentarsi un reale già solo a 4 dimensioni.
La grande idea di Spock (che semplificava il problema) consisteva nell'”aiutino” che vi abbiamo dato. Come dicevamo, se consideriamo le due astronavi e il centro del sistema sullo stesso piano (per tre punti distinti nello spazio passa un solo piano) e consideriamo questo piano fisso, la soluzione è perfettamente identica.
Supponiamo che il rapporto tra le due velocità sia a e il raggio del sistema r; la strategia di Spock potrebbe essere:
1. Muoversi lungo un’orbita con raggio r/a-d concentrico con il sistema sin quando non si trova diametralmente opposto ai Klingon.
2. Muoversi lungo una linea radiale per una distanza d verso il bordo del sistema opposto ai Klingon
3. Verificare da che parte girano i Klingon per girare attorno al sistema e deviare ad angolo retto nella direzione opposta.
4. Se i Klingon cambiano direzione, tornare al punto [2], altrimenti continuare sin quando non si raggiunge la riva e via a Curvatura nove!
Il valore deve essere abbastanza piccolo da permettere comunque la fuga; la chiave di questa strategia è che l’Enterprise segue un cammino radiale che la allontana dai Klingon sin quando questi non decidono da che parte girare; in questo momento, l’Enterprise inizia un nuovo percorso che interseca il bordo del sistema ad una distanza maggiore della semicirconferenza rispetto alla posizione e al verso del moto attuale dei Klingon; in pratica, l’Enterprise si muove sulla tangente ad un cerchio di raggio r/a.
Se definiamo:
t = arccos(1/a)
abbiamo che l’Enterprise deve percorrere una distanza:
LE = rsin t + d
Mentre i Klingon, forzati fuori del sistema, devono percorrere uno spazio:
LK = r (PIGRECO + t) – ad
Se d tende a zero, l’Enterprise riuscirà a fuggire solo se è:
r (PIGRECO + t) < ar sin t
ossia (semplificando r, trasformando il seno in radice di uno meno coseno quadro e utilizzando il valore di arcoseno imposto sopra)
…e qui, come vi dicevamo, viene comodo Data.
Un foglio elettronico sul quale tabuliate la funzione, comunque, vi mostra che anche se l’astronave dei Klingon è quattro volte e mezzo più veloce di voi, riuscite a scappare; il valore critico per a risulta infatti 4,605…
E siamo pronti per un’altra “Data Astrale…”
